Пошаговое объяснение:
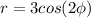
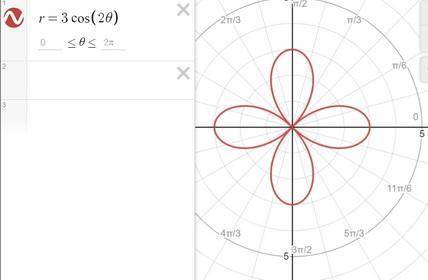
это полярная роза. поскольку аргумент для cos четный, то тут будет 4 лепестка.
из графика видим, что для половины лепестка аргумент изменяется
от 0 до п/4
нам надо найти площадь 1/2 лепестка и умножить ее на 8, т.е наша площадь будет
S= 8*S₁
площадь половины лепестка находим по формуле площади криволинейного сектора
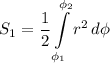
для нас будет (заметим, что при замене переменных для вычисления будут меняться и пределы интегрирования)
![\displaystyle S_1=\frac{1}{2} \int\limits^{\pi/4}_0 {(3cos(2\phi))^2} \, d\phi =\frac{9}{2} \int\limits^{\pi/4}_0 {cos^2(2\phi)} \, d\phi=\left[\begin{array}{ccc}u=2\phi\quad du=2d\phi\\u_1=0\hfill\\u_2=\pi/2\hfill\end{array}\right] =](/tpl/images/2008/4191/38d69.png)
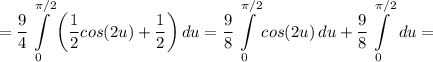
![\displaystyle =\frac{9}{8} \left[\begin{array}{ccc}s=2u\quad ds=2du\\s_1=0\hfill\\s_2=\pi\hfill\end{array}\right] +\frac{9u}{8} \bigg |_0^{\pi/2}=\frac{9}{16} \int\limits^\pi_0 {cos(s)} \, ds+\frac{9u}{8} \bigg |_0^{\pi/2}=](/tpl/images/2008/4191/580df.png)
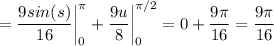
итак, мы вычислили 1/2 лепестка розы. теперь узнаем всю площадь нашей полярной розы
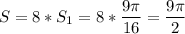
это и есть ответ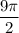 
условных единиц.
Диагональ прямоугольника делит его на два равных прямоугольных треугольника. Возьмем один из них. Его гипотенуза - это диагональ прямоугольника, равная 15. Его катеты - это стороны прямоугольника, которые по условию относятся как 3:4. Вспоминаем прямоугольный треугольник, который встречается чаще всего - это египетский треугольник 3-4-5. Наш треугольник будет подобен ему, а так как у нашего треугольника гипотенуза в три раза больше, чем у египетского, коэффициент подобия равен трем, а тогда катеты нашего треугольника будут 3·3=9 и 4·3=12. Ну а тогда периметр прямоугольника равен 2(9+12)=42.
Если Вы не знакомы с египетским треугольником, ничего страшного, давайте обойдемся без него. По условию катеты равны a=3t и b=4t. По теореме Пифагора (3t)²+(4t)²=15²; 25t²=5²·3^2; t=3; a=9; b=12.
1) 354*7=2478
2) 437*8=3496
3) 964*6=5784
4) 1743+2151=3894
5) 3894+4731=8625
6) 8625+14152=22777
7) 22777+31737=54514
8) 54514-2478=52036
9) 52036+3249=55285
10) 55285+3496=58781
11) 58781-5784=52997