Пусть в рулоне х метров ткани.
1) На пошив пододеяльника ушло 0,4 рулона без 6 метров:
0,4х-6
Тогда осталось: х-(0,4х-6)=х-0,4х+6=0,6х+6 метров ткани.
2) На пошив простыни ушло без 4 метров 0,6 от остатка рулона: (0,6х+6)*0,6-4=0,36х+3,6-4=0,36х-0,4
После этого осталось: (0,6х+6)- (0,36х-0,4) =0,6х+6 -0,36х+0,4=0,24х+6,4 метров ткани.
3) На наволочки ушло 0,75 без 3 метров от нового остатка: (0,24х+6,4)*0,75-3=0,18х+4,8-3=0,18х+1,8
В рулоне осталось 10 метров ткани.
Составим и решим уравнение:
х - (0,4х-6)-(0,36х-0,4)-( 0,18х+1,8)=10
х-0,4х+6-0,36х+0,4-0,18х-1,8=10
0,06х+4,6=10
0,06х=10-4,6
0,06х=5,4
х=5,4:0,06
х=90 метров ткани в рулоне
На пошив пододеяльников ушло:
0,4х-6=0,4*90-6=30 метров ткани.
На пошив простыней ушло:
0,36х-0,4=0,36*90-0,4=32 метра ткани
(или 90-30=60; 60*0,6-4=32 метра ткани)
На наволочки ушло:
0,18х+1,8=0,18*90+1,8=18 метров ткани
(или 60-32=28; 28*0,75-3=18 метров ткани).
90-(30+32+18)=10
ответ: 1) в рулоне было 90 метров ткани; 2) на пошив пододеяльников ушло 30 метров ткани, простыней - 32 метра ткани.
Пусть х м в рулоне, тогда распишем по условию задачи расходы и остатки от пошива постельного белья:
Пододеяльник :
расход: 0,4 х - 6 (м)
остаток после пошива: х-0,4х+6 = 06 х +6 (м)
Простынь:
расход: 0,6(0,6х+6) - 4 = 0,36х+3,6-4=0,36х-0,4 (м)
остаток после пошива: 0,6х+6-0,36х+0,4=0,24х+6,4 (м)
Наволочка:
расход: (0,24х+6,4)*0,75-3=0,18х+4,8-3=0,18х+1,8 (м)
остаток после пошива:0,24х+6,4-0,18х-1,8=0,06х+4,6
Так как по условию задачи остаток составил 10 м, то составляем уравнение:
0,06х+4,6=10
0,06х = 5,4
х=5,4 : 0,06
х= 54 : 0,6
х=90 (м) в рулоне было
2) 0,36 * 90 -0,4= 32 (м) ушло на простыни
3) 0,4*90-6=36-6=30 (м) ушло на пододеяльники
4) 0,18*90+1,8=18 (м) ушло на наволочки
Проверка:
30+32+18= 80 (м) ушло на пошив
90-80 = 10 (м) остаток ткани
1) y=x^2+x-6x=x^2-5x, где x>=0
график - парабола, ветви вверх.
вершина : x=5/2=2,5; y=-6,25; (2,5;-6,25)
точки пересечения с осями координат:
x=0; y=0; (0;0)
y=0; x^2-5x=0; x(x-5)=0; x1=0; x2=5
(5;0)
2 точки
найдем еще какие-нибудь точки:
x=1; y=-4; (1;-4)
x=2; y=-6; (2;-6)
строим график этой функции на интервале [0;+oo)
2)y=-x^2-x-6x=-x^2-7x, где x<=0
график - парабола, ветви вниз.
вершина: x=7/(-2)=-3,5; y=-12,25+24,5=12,25 (-3,5;12,25)
точки пересечения с осями координат:
x=0; y=0; (0;0)
y=0; -x^2-7x=0; x(x+7)=0; x1=0; x2=-7
(-7;0)
найдем еще какие-нибудь точки:
x=-1; y=-1+7=6; (-1;6)
x=-2; y=-4+14=10; (-2;10)
строим график функции на промежутке (-oo;0]
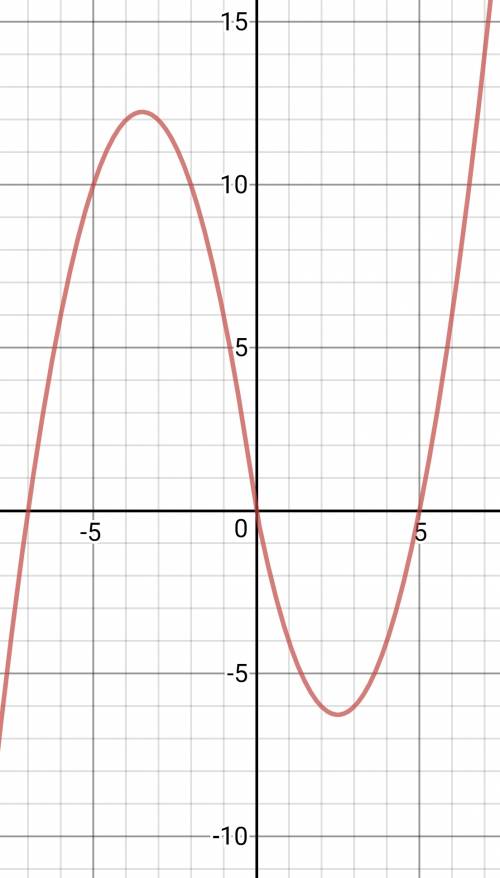
График в приложении.
По нему видно, что прямая y=m будет иметь с графиком 2 общие точки если будет проходить либо через вершину 1 параболы, либо через вершину 2, берем y-координаты вершин, это и будут нужные нам значения m: m1=-6,25; m2=12,25