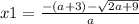
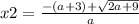
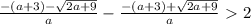
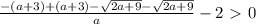
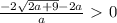
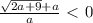
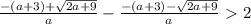
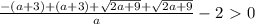
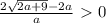
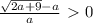
1. а) На 5 делятся числа, которые кончаются на 5 и на 0.
4875, 2520, 1270.
б) На 9 делятся числа, у которых сумма цифр делится на 9.
4+8+7+5 = 24 - нет.
2+5+2+0 = 9 - да.
1+2+7+0 = 10 - нет.
1+7+1+9 = 18 - да.
в) На 10 делятся числа, которые кончаются на 0.
2520 и 1270.
2. а) 126/318 = 21/53. б) 330/390 = 33/39 = 11/13.
3. Белых роз 25, красных 25*3 = 75, желтых 25+15 = 40.
5 одинаковых букетов по 5 белых роз, 15 красных и 8 желтых.
4. 21mn / (7m) = 21/7 * mn/m = 3*n
5. После того, как одна библиотека передала другой 60 книг, стало всего 792 книги, и во 2-ой библиотеке в 2 раза больше, чем в 1-ой.
Значит, в 1-ой библиотеке стало 792/3 = 264 книги, во 2-ой 528 книг.
Это после того, как 1-ая библиотека передала 2-ой 60 книг.
Значит, сначала было в 1-ой 264+60 = 324 книги, а во 2-ой 468 книг.
1. а) На 5 делятся числа, которые кончаются на 5 и на 0.
4875, 2520, 1270.
б) На 9 делятся числа, у которых сумма цифр делится на 9.
4+8+7+5 = 24 - нет.
2+5+2+0 = 9 - да.
1+2+7+0 = 10 - нет.
1+7+1+9 = 18 - да.
в) На 10 делятся числа, которые кончаются на 0.
2520 и 1270.
2. а) 126/318 = 21/53. б) 330/390 = 33/39 = 11/13.
3. Белых роз 25, красных 25*3 = 75, желтых 25+15 = 40.
5 одинаковых букетов по 5 белых роз, 15 красных и 8 желтых.
4. 21mn / (7m) = 21/7 * mn/m = 3*n
5. После того, как одна библиотека передала другой 60 книг, стало всего 792 книги, и во 2-ой библиотеке в 2 раза больше, чем в 1-ой.
Значит, в 1-ой библиотеке стало 792/3 = 264 книги, во 2-ой 528 книг.
Это после того, как 1-ая библиотека передала 2-ой 60 книг.
Значит, сначала было в 1-ой 264+60 = 324 книги, а во 2-ой 468 книг.
Два корня будет, если дискриминант будет больше нуля:
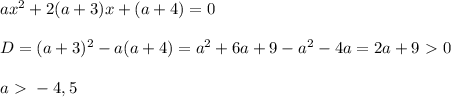
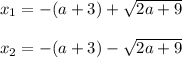
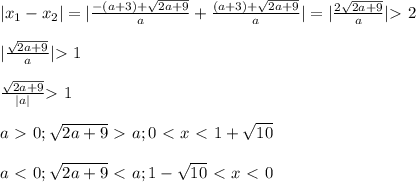
Также один корень будет, если а = 0 и квадратное уравнение превратится в линейное.
Расстояния между корнями больше 2. Напишем сначала, чему равны корни:
Найдём модуль разницы между корнями - это и будет искомое расстояние:
ответ: a ∈ (1- \sqrt{10}; 0) ∪ (0; 1+ \sqrt{10})