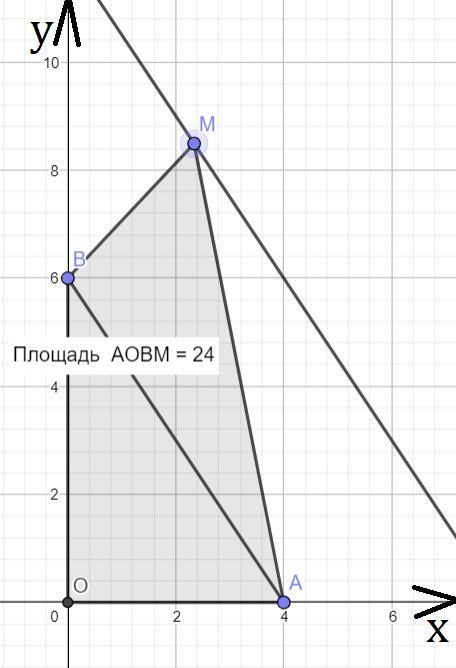
Прямая проходящая через точки A, B имеет уравнение:
y=ax+t, подставим координаты точек чтобы найти уравнение в явном виде.
6=a·o+t ⇒ t=6; 0=a·4+t ⇒ a=-6/4=-1,5
y = -1,5x+6
Исходя из последовательности вершин четырёхугольника, получаем, что координаты M(x;y) удовлетворяют неравенству y≥-1,5x+6.
Заметим, что S(AOBM) = S(AOB)+S(BMA), при этом S(AOBM)=24, S(AOB)=AO·OB/2=12.
Тогда S(BMA)=12.
Поскольку площадь треугольника постоянная и длина стороны AB тоже. То высота опущенная из M на AB должна быть постоянной, откуда M лежит на прямой параллельной AB. Тогда угол наклона k равен углу наклона прямой проходящей через точки A, B.
k = -1,5
ответ: -1,5.
Дано:
R = 1 см (радиус большого шара)
r = 0,5 см (радиус малых шариков)
π ≈ 3
Найти: n (число полученных малых шариков)
Формула объёма шара: Vш=(4/3)πr³
Так как малые шарики изготовят из того же объёма металла, что был в большом шаре, то просто делим объём большого шара на объём маленького шарика (а затем берём целую часть полученного числа, а дробную- отбрасываем).
Можно решать, сразу выполняя деление (много можно сократить):
Vбольш.ш / Vмал.ш = (4/3)πR³ / ((4/3)πr³) = R³ / r³ = (R / r)³ = (1 / 0,5)³ = 2³ = 8
Результат и так целый, то есть n = 8 (шариков)
Либо, можно отдельно найти объёмы шаров и затем делить:
Vбольш.ш = (4/3)πR³ = (4/3)·3·1³ = 4·1 = 4 см³
Vмал.ш = (4/3)πr³ = (4/3)·3·0,5³ = 4·0,125 = 0,5 см³
Vбольш.ш / Vмал.ш = 4 / 0,5 = 8
n = 8 (шариков)
ответ: n = 8
Находим наибольший коэффициент в слагаемых функции.
Коэффициенты: (1/2)³ = 1/8 и 4.
E(f) = +/- 4 или E(f)∈(-4;4) - ОТВЕТ