Пусть N имеет натуральные делители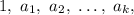 
и их сумма равна A. Пусть, кроме того, 
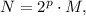где N - нечетное число.
Четные делители числа N имеют вид
Складывая четные делители группами в соответствие с тем, сколько множителей вида 2 в них есть, а потом складывая эти группы, получим
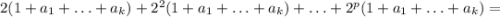
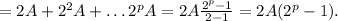
Требуется проверить, может ли
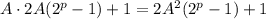
быть полным квадратом, то есть равняться B².
Конечно, такого быть не может, так как если перенести 1 направо, мы получили бы
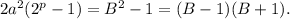
Выражение, стоящее слева, делится на 2, но не делится на 4, выражение же, стоящее справа, или является нечетным (если B четное), или же делится не только на 4, а даже на 8 (хотя нам это и не нужно) -- ведь из двух последовательных четных чисел одно обязательно делится на 4.
ответ:Понятие площади: это величина той части плоскости, которую занимает фигура. Выражается положительным числом, которое зависит от выбора единицы измерения.
Свойство 1. Площадь фигуры является неотрицательным числом.
Свойство 2. Площади равных фигур равны.
Свойство 3. Если фигура разделена на две части, то площадь всей фигуры равна сумме площадей образовавшихся частей.
Еще нужна фигура, которую мы примем за эталон для измерения площади, ¾ единицу площади. При этом не следует забывать, что уже имеется единица измерения длины.
Свойство 4. За единицу измерения площади принимается площадь квадрата со стороной, равной 1 единице длины.
Другими словами, площадь квадрата со стороной, равной 1 единице длины, равна 1 единице площади, или 1 квадратной единице. Например, площадь квадрата со стороной 1 метр равна одному квадратному метру
Фигуры, имеющие равные площади, называется равновеликими.
перевод: Мне очень нравится моя школа. У неё четыре этажа, и на каждом из них находятся уютные кабинеты. Каждый из них очень красив и привлекателен. Ещё имеется спортивный зал. Он очень большой. И столовая. В ней всегда много народу. Учителя в нашей школе очень добры и приветливы. Большинство из них - женщины. Вот такая нашая школа