Надеюсь, что правильно:-)

lg 2x < lg (x+1)
ОДЗ:
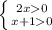
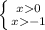
x∈(0;+∞)
lg 2x < lg (x+1)
2x < x + 1
x < 1
С учетом ОДЗ:
x∈(0;1)
ответ: x∈(0;1)
№ 2log2(1-x) < 1
ОДЗ:
1-x>0
x<1
x∈(-∞;1)
log2(1-x) < 1
log2(1-x) < log2(2)
1-x<2
x>-1
С учетом ОДЗ:
x∈(-1;1)
ответ: x∈(-1;1)
№ 3(log3(x) - 2)*sqrt(x^2-4)<=0
ОДЗ:
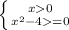
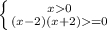
x∈[2;+∞)
(log3(x) - 2)*sqrt(x^2-4)<=0
Т.к. sqrt(x^2-4) - всегда >= 0, то выражение будет < нуля в случае, когда log3(x) - 2 < 0 => Равносилен переход к совокупности:
log3(x) - 2 <= 0 или sqrt(x^2-4)=0
log3(x) <= 2 или (x-2)(x+2)=0
log3(x) <= log3(3^2) или x = ± 2
x <= 9 или x = ± 2
С учетом ОДЗ:
x∈[2;9]
ответ: x∈[2;9]
Пошаговое объяснение:
(3 5/6 - 2 3/4) : 7/12 +5 1/2= 7 5/14
3 5/6-2 3/4=3 10/12-2 9/12=1 1/12
1 1/12:7/12=13/12*12/7=13/7=1 6/7
1 6/7+5 1/2=1 12/14+5 7/14=7 5/14
2 2/3(2 1/3 + 2 5/12) - 4 4/5= 7 13/15
2 1/3+2 5/12=2 4/12+2 5/12=4 3/4
2 2/3*4 3/4=8/3*19/4=38/3=12 2/3
12 2/3-4 4/5=12 10/15-4 12/15=7 13/15