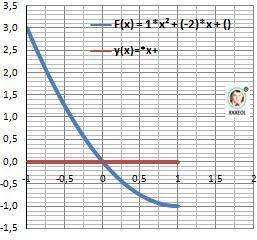
Дано: F(x) = x² -2*x , y(x)=0, а = -1,
b = 1
Найти: S=? - площадь фигуры
b = 1 - верхний предел, a = -1 - нижний предел.
2) Площадь - интеграл разности функций. Прямая выше параболы.
s(x) = y(x) - F(x) =2*x - x² - подинтегральная функция
3) Интегрируем функцию и получаем:
S(x) = (2)/2*x² -1/3*x³
4) Вычисляем на границах интегрирования.
S(а) = S(-1) = 1 + 1/3 = 4/3 (1.33)
S(b) = S(1) = 1 - 1/3 = 2/3 (0.67)
ВАЖНО! Площади с двух сторон от оси ОХ - сумма площадей.
S = S(-1) + S(1) = 4/3 + 2/3 = 2 (ед.²) - площадь - ответ
Рисунок к задаче в приложении.
Г и Д
Пошаговое объяснение:
5 - 2 = 3. Т.е. 3 жителя являются рыцарями, если по условию 2 лжеца из 5.
1) Если А - лжец, то лжец Б, который назвал А рыцарем, и В, который назвал рыцарем Б, и , далее, Г и Д, т.к. каждый называет рыцарем себя и предыдущего. Получается, что все - лжецы. Противоречие. Значит, А - действительно рыцарь.
2) Если Б лжец, то лжец В, считающий его и себя рыцарем, и Г, считающий рыцарем В, и Д, считающий рыцарем Г. Но 4 лжеца противоречат условию, Значит, Б - тоже рыцарь
3) Если В - лжец, то лжец Г, считающий его рыцарем, и Д, считающий рыцарем Г, значит, В говорит правду и он - рыцарь.
4) Имеем ужу 3 рыцаря - А, Б, В, значит, Г и Д - лжецы, так как по условию имеются 2 лжеца.
5) Г сказал: «И я, и В – мы оба рыцари.» И он солгал, что оба, а на самом деле рыцарь только В. Т.е. противоречий в том, что Г лжец нет
6) Д сказал: «И я, и Г – мы оба рыцари.»Противоречий к тому, что это ложь нет.
ответ: Г и Д - лжецы.