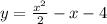
Выполним построение опираясь на геометрический смысл производной и не только. Для начала найдём все пересечения с осями координат.
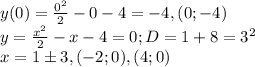
Выделим полный квадрат.
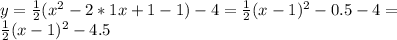
Из этого следует, что для (x-1) функция чётная, то есть имеет вертикальную ось симметрию, поэтому для нашей функций x=1 это вертикальная ось симметрии.
Теперь найдём первую производную.
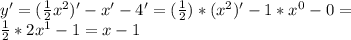
Если x>1, то производная положительная, значит функция возрастает.
Если x<1, то производная отрицательная, значит функция убывает.
При х=1, производная равна нулю и меняет свой знак с минуса на плюс, поэтому это минимум функции.
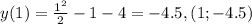
Теперь найдём вторую производную.
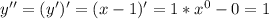
Как видно производная всегда всегда положительная, поэтому функция всегда выпукла вниз.
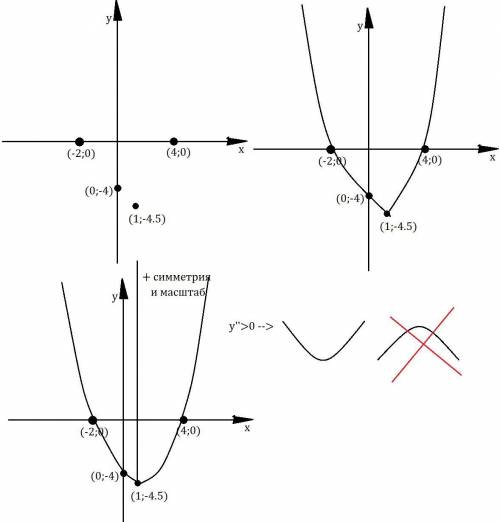
Смотри построение внизу.
Произведения M1*D1, M1*D2, M2*D1, M2*D2.
Сумма двух произведений равна сумме двух других произведений.
Возможные варианты:
1) M1*D1 + M1*D2 = M2*D1 + M2*D2
M1*(D1 + D2) = M2*(D1 + D2)
Отсюда M1 = M2, но по условию Маша написала 2 различных числа.
Значит, этот вариант не подходит.
2) M1*D1 + M2*D1 = M1*D2 + M2*D2
D1*(M1 + M2) = D2*(M1 + M2)
Теперь получилось, что D1 = D2, но это тоже невозможно.
3) M1*D1 + M2*D2 = M1*D2 + M2*D1
M1*D1 - M1*D2 = M2*D1 - M2*D2
M1*(D1 - D2) = M2*(D1 - D2)
Теперь опять получилось, что M1 = M2, или D1 = D2.
ответ: Это может случиться, только если одна из девочек, или обе, напишет два одинаковых числа.