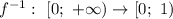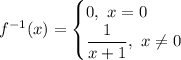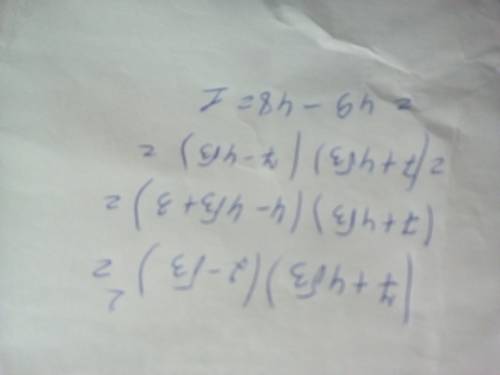
1. Если перемножить числа 7,11 и 13, то получим:
7*11*13=1001
2. При умножении числа 1001 на любое трехзначное число получается результат, состоящий из этого трехзначного числа, только написанного дважды:
873*1001=873873, 205*1001=205205 и т.д., т.е. получаем шестизначное число, в котором первая цифра совпадает с четвёртой, вторая с пятой, третья с шестой, а т.к. один из множителей (1001) - делится на 7,11 и 13, то и все произведение (шестизначное число) - будет делиться на 7,11 и 13, что и требовалось доказать.
Рассмотрим промежуток 
.
Заметим, что при нахождении обратных чисел для чисел из этого промежутка, мы будем однозначно получать числа из промежутка 
.
Рассмотрим промежуток .
Заметим, что если мы будем находить числа, на 1 меньшие, чем числа из данного промежутка, мы будем однозначно получать числа из промежутка 
.
Таким образом, по некоторому числу из промежутка однозначно определяется число из промежутка .
Получим отображение:
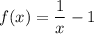
Рассуждая в обратном направлении можно получить обратное отображение. Прибавляя 1 к некоторому числу из промежутка , а затем находя для получившегося числа обратное, мы будем однозначно получать числа из промежутка .
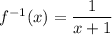
Но по условию вместо промежутка рассматривается промежуток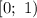 
, а вместо промежутка - промежуток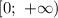 
. Тогда, сопоставим нули в этих промежутках друг другу.
Получим прямое отображение:
Получим обратное отображение:
