1. На первое место можно использовать 6 цифр, на второе место - оставшиеся 5 цифр, на третье место - оставшиеся 4 цифр, на четвертое место - 3 цифры, на пятое место - 2 цифры, на последнее место - одна оставшаяся цифра. По правилу произведения, составить шестизначных чисел можно
2. Порядок выбора учащихся не имеет значения, поэтому выбрать двух учащихся для участия в городской олимпиаде можно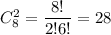 
3. Дежурного можно выбрать а его По правилу произведения это можно сделать.
4. Всего всевозможных элементарных исходов 30 из них благоприятствуют только 30-5=25 элементарных исходов, т.е.
m = 25
n = 30
Вероятность того, что она не окажется учебником, равна 25/30 = 5/6
5. Выбрать две книги можно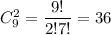 
а три журнала - 
По правилу произведения можно сделать этот выбор.
6. Всего всевозможных элементарных исходов: 5! = 120 слов из них благоприятствуют только два слова: "конус" или "сукно".
n = 120
m = 2
Вероятность того, что в результате получится слово "конус" или "сукно", равна 2/120 = 1/60
1)вероятность вытащить окрашенную деталь 7/10=0.7, вероятность вытащить неокрашенную => 0.3. Набор деталей, которые надо взять конкретен: и окрашенные, и неокрашенные. За логическую операцию и отвечает умножение => умножим вероятности:
0.7*0.7*0,3=0,147
2) теперь вычислим вероятность взять две неокрашенные детали и одну окрашенную:
0,3*0,3*0,7=0,063
3) теперь вычислим с какой вероятностью можно вытащить 3 неокрашенные детали:
0,3*0,3*0,3=0,027
Нам нужен или первый исход, или второй, или третий. За логическую операцию или отвечает сложение => для нахождения общей сложим вероятности трёх удачных исходов:
0,147+0,063+0,027=0,237
ответ: вероятность вытащить не более двух окрашенных деталей равна 23,7%