Считаем площадь фигуры между двумя графиками по формуле
S= \int\limits^a_b {((f(x)-g(x))} \, dxS=
b
∫
a
((f(x)−g(x))dx ,
где f(x)- кривая, график, которой расположен выше кривой у=g(x);
a и b - абсциссы точек пересечения графиков; a<b.
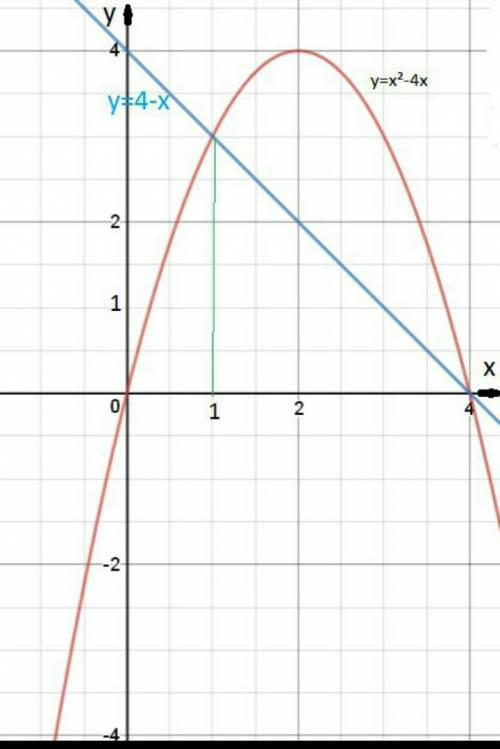
Строим графики функций ( см. рис. в приложении):
у=4х-х²- парабола, ветви которой направлены вверх, точки пересечения с осью Ох:
х=0; х=4
Координаты вершины (2;4).
у=4-х - прямая, проходящая через точки (0;4) и (4;0).
Находим абсциссы точек пересечения графиков функций:
4х-х²=4-х;
х²-5х+4=0
D=25-4·4=9
x=(5-3)/2=1 или х=(5+3)/2=4
\begin{gathered}S= \int\limits^4_1 {((4x- x^{2})-(4-x))} \, dx= \\ \\ =\int\limits^4_1 {(4x- x^{2}-4+x)} \, dx= \\ \\ = \int\limits^4_1 {(5x- x^{2}-4)} \, dx= \\ \\ =( 5\cdot \frac{ x^{2} }{2} - \frac{x^3}{3}-4x)| ^4_1= ( 5\cdot \frac{ 4^{2} }{2} - \frac{4^3}{3}-4\cdot 4)-( 5\cdot \frac{ 1^{2} }{2} - \frac{1^3}{3}-4)=\end{gathered}
S=
1
∫
4
((4x−x
2
)−(4−x))dx=
=
1
∫
4
(4x−x
2
−4+x)dx=
=
1
∫
4
(5x−x
2
−4)dx=
=(5⋅
2
x
2
−
3
x
3
−4x)∣
1
4
=(5⋅
2
4
2
−
3
4
3
−4⋅4)−(5⋅
2
1
2
−
3
1
3
−4)=
40 - \frac{64}{3}-16- \frac{5}{2} + \frac{1}{3}+4=4,540−
3
64
−16−
2
5
+
3
1
+4=4,5
кв. ед.
О т в е т. S=4,5 кв. ед.
36 - Сын + 40 - Сын = 60
76 - 2 Сын = 60
2 Сын = 76-60
2 Сын = 16
Сын = 16:2
Сын = 8 (лет) - возраст сына.
Отец = 40 - Сын = 40-8=32 (года) - возраст отца.
Мать = 36 - Сын = 36-8=28 (лет) - возраст матери Предположим, что возраст сына х лет, тогда возраст матери (36-х) лет, а возраст отца (40-х) лет, также из условия задачи известно, что отцу и матери вместе 60 лет
согласно этим данным составим и решим уравнение:
36-х+40-х=60
76-2х=60
2х=76-60
2х=16
х=16:2
х=8 (лет) – возраст сына.
36-х=36-8=28 (лет) – возраст матери.
40-х=40-8=32 (года) – возраст отца лет) - возраст сына.
2) 40-8=32 (года) - возраст отца.
3) 36-6=28 (лет) - возраст матери.
ответ: сыну 8 лет; матери - 28 лет; отцу - 32 года.
А) 1,9(32) = 1 + 0,9(32) = 1 целая 923/990
Пусть х = 0,93232..., тогда
10х = 9,3232...
1000х = 932,3232...
Уравнение:
1000х - 10х = 932 - 9
990х = 923
х = 923/990
Б) 9,(1) = 9 целых 1/9