Скорость теплохода в неподвижной воде 12 км/ч.
Пошаговое объяснение:
Пусть собственная скорость теплохода (т.е. скорость в неподвижной воде) = x км/ч. По условию скорость течения реки = 2 км/ч.
1) По течению реки теплоход шел со скоростью υ = x + 2 км/ч путь S = 70 км, за время 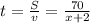 часа.
часа.
2) Против течения реки теплоход шел со скоростью υ = x - 2 км/ч путь S = 70 км, за время 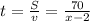 часа.
часа.
3) Так как стоянка длилась 8 часов, то время движения теплохода составляет 20 ч - 8 ч = 12 часов.
Составим уравнение и решим его:
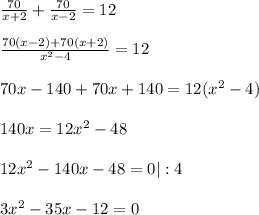
D = b² - 4ac = 35² + 4 * 3 * 12 = 1225 + 144 = 1369 = 37²
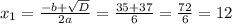 (км/ч)
(км/ч)
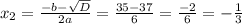 (не является решением задачи)
(не является решением задачи)
Скорость теплохода в неподвижной воде 12 км/ч.
Вероятность вынуть из второй урны 4 белых шара: 6С4/14С4 = 6!/(4!•2!) • 4!•10!/14! = 3•4•5•6/(11•12•13•14) = 5•6/(11•13•14) = 5•3/(11•13•7) = 15/1001.
Вероятность этого события: 5/14 • 15/1001 = 75/14014
Вероятность вынуть из первой урны 2 белых шара и 1 чёрный: 6С2•2С1/8С3 = 6!/(2!•4!) • 2 • 3!•5!/8! = 5•6•6/(6•7•8) = 5•3/7•4 = 15/28.
Вероятность вынуть из второй урны 4 белых шара: 5С4/14С4 = 5!/(4!•1!) • 4!•10!/14! = 5•24/(11•12•13•14) = 5/(11•13•7) = 5/1001.
Вероятность этого события: 15/28 • 5/1001 = 75/28028.
Вероятность вынуть из первой урны 1 белый шар и 2 чёрных: 6С1•2С2/8С3 = 6 • 1 • 3!•5!/8! = 6•6/(6•7•8) = 3/7•4 = 3/28.
Вероятность вынуть из второй урны 4 белых шара:4С4/14С4 = 1 • 4!•10!/14! = 24/(11•12•13•14) = 1/(11•13•7) = 1/1001.
Вероятность этого события: 3/28 • 1/1001 = 3/28028.
Вероятность вынуть из второй урны 4 белых шара: 75/14014 + 75/28028 + 3/28028 = 228/28028 = 57/7007