У(x)=(х^2-4)/(x-3) 1)ОДЗ x-3 не равно 0 -> x є (-беск ; 3) U (3;+беск) 2)график имеет вертикальную асимптоту х=3 3)нули функции у(x)=(х^2-4)/(x-3)=(х-2)*(х+2)/(x-3)=0 при х=-2 и при х = 2 4)асимптота вида у = ах+в у(x)=(х^2-4)/(x-3) = у=(х^2-3х+3х-12+12-4)/(x-3) = х + 3+ 8/(х-3) a = lim y(x)/x = lim( (х + 3+ 8/(х-3)) : x ) = 1 b = lim (y(x) - a*x) = lim (х + 3+ 8/(х-3) - 1*x) = lim ( 3+ 8/(х-3)) = 3 наклонная асимптота вида у = ах+в у=х+3 5)экстремумы у(x)= х + 3+ 8/(х-3) у`(x)= 1 - 8/(х-3)^2 у`(x)=0 при х=3 + (+/-) корень(8) x1 =3 - корень(8) x2 =3 + корень(8) у``(x)= 16/(х-3)^3 у``(x1)= 16/(х1-3)^3=-16/(8)^(3/2) < 0 -> x1 - точка локального максимума у``(x2)= 16/(х2-3)^3=16/(8)^(3/2) > 0 -> x2 - точка локального максимума 6)перегибы уравнение у``(x)= 16/(х-3)^3=0 - не имеет решений -> график перегибов не имеет 7)четность у(-х)=((-х)^2-4)/((-x)-3) = -(х^2-4)/(x+3) у(-х) - не равно у(х) у(-х) - не равно -у(х) функция у(х) не является ни четной ни нечетной 8) не периодичная так как имеется ограниченное и ненулевое число экстремумов
Возьмём два наполовину заполненных бидона, их суммарный вес 37 кг, а именно18,500+18,500=37 (кг)Перельём всё молоко в один бидон. Получим полный бидон (35 кг) и пустой бидон. Следовательно, что пустой бидон весит 37-35=2 (кг Предположим, что вес бидона - х кг, тогда вес молока в полном бидоне (35-х) кг, а вес наполовину заполненного бидона масса наполовину заполненного молоком бидона 18,5 кгсогласно этим данным составим и решим уравнение:0,5(35-х)+ х=18,517,5+0,5х=18,5 0,5х=18,5-17,50,5х=1х=1:0,5х=2 (кг) - масса пустого бидона. кг=1 000 г ⇒ 35 кг=35 000 г ⇒ 18кг 500г=18 500 г 18 500+18 500=37 000 (г) или 18 500·2=37 000 (г) или 37 (кг) 37 000-35 000=2 000 (г) или 2 (кг) - масса пустого бидона.ответ : 2 кг весит пустой бидон.
1. 4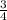 -1
-1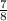 =
=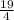 -
-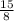 =
=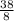 -
-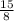 =
=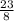 (км турист за второй час;
(км турист за второй час;
2. 4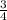 +
+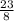 =
=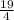 +
+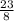 =
=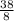 +
+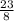 =
=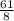 =7
=7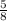 (км) -преодолел турист за два часа.
(км) -преодолел турист за два часа.
ответ: 7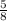 км преодолел турист.
км преодолел турист.