Все что могла решила)

![t^2 - 8 t + [7-a] = 0 ,](/tpl/images/0495/7941/4dac0.png) где под
где под 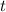 подразумевается квадрат переменной
подразумевается квадрат переменной 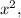 т.е.
т.е.  а его корнями
а его корнями 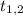 – квадраты искомых корней, если они различны, или его чётным корнем
– квадраты искомых корней, если они различны, или его чётным корнем 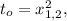 если корень биквадратного трёхчлена
если корень биквадратного трёхчлена 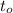 – единственный.
– единственный.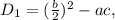 тогда
тогда ![D_1 = 4^2 - [7-a] = 9 + a .](/tpl/images/0495/7941/d229f.png) Потребуем, чтобы
Потребуем, чтобы 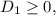 откуда следует, что
откуда следует, что 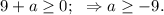
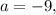 а корень биквадратного трёхчлена станет чётным
а корень биквадратного трёхчлена станет чётным  давая два искомых корня
давая два искомых корня 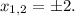 Это значение
Это значение 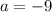 как раз уже и есть одно из искомых решений для параметра
как раз уже и есть одно из искомых решений для параметра 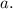
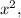 всегда будет два – левый и правый (меньший и больший), однако при некоторых обстоятельствах левый квадрат искомых корней будет отрицательным, а значит, не будет давать пару искомых корней. Среднеарифметическое квадратов искомых корней
всегда будет два – левый и правый (меньший и больший), однако при некоторых обстоятельствах левый квадрат искомых корней будет отрицательным, а значит, не будет давать пару искомых корней. Среднеарифметическое квадратов искомых корней 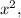 по теореме Виета, в применении к биквадратному уравнению, будет равно числу, противоположному половине среднего коэффициента, т.е. оно равно
по теореме Виета, в применении к биквадратному уравнению, будет равно числу, противоположному половине среднего коэффициента, т.е. оно равно 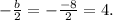 Отсюда следует, что правый квадрат искомых корней
Отсюда следует, что правый квадрат искомых корней 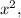 – всегда положителен, а значит, всегда даёт два корня при положительном дискриминанте.
– всегда положителен, а значит, всегда даёт два корня при положительном дискриминанте.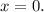 А значит, значение всего трёхчлена
А значит, значение всего трёхчлена ![x^4 - 8 x^2 + [7-a]](/tpl/images/0495/7941/7bbf9.png) взятое от
взятое от 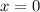 должно давать отрицательное значение, т.е. располагается в нижней межкорневой дуге параболы биквадратного трёхчлена.
должно давать отрицательное значение, т.е. располагается в нижней межкорневой дуге параболы биквадратного трёхчлена.![0^4 - 8 \cdot 0^2 + [7-a] < 0](/tpl/images/0495/7941/13440.png) ;
; ;
;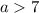 ;
;
1) 7 1/6 - 6 5/24 (приводим к общему знаменателю) = 7 4/24 - 6 5/24 = 23/24
2) 9 - 3/7 = 8 7/7 - 3/7 = 8 4/7
3) 16 - 8 3/5 = 15 5/5 - 8 3/5 = 7 2/5
4) 6 5/16 - 4 11/30 (приводим к общему знаменателю) = 6 150/480 - 4 176/480 = 1 454/480 = 1 227/240
5) 7 5/16 - 3 1/6 (приводим к общему знаменателю) = 7 15/48 - 3 8 /48 =
4 7/48
6) 14 1/6 - 5 4/9 + 6 2/3 (приводим к общему знаменателю) = 14 3/18 - 5 8/18 + 6 12/18 = 8 16/18 + 6 12/18 = 15 10/18 = 15 5/9