Прекрасный закат красит небесный свод интересными красками. По ясному небу проплывают маленькие курчевые облачка. В лучах заходящего солнца они становятся разноцветными. На этом фоне Кружат ласточки и стрижи. Они делают свои последние сегодняшние вылеты и ловят вечернюю мошкару. Но приблнжается поздний вечер. Солнечный диск уже давно исчез за верхушками деревьев. А чудесная расцветка держится в темнеющем небе. И вот в свои права властно вступает звёздная ночь. Совсем стемнело. Вечернее время кончилось. Небо украсилось острым, блестящим месяцем. Порой его тонкие кончики прячутся в тёмной дымке, но почти сразу появляются снова и сияют во всю свою мощь.
ответ: 26; 15; 64;250;24
Пошаговое объяснение:
Делаем задания через определенные интегралы и первообразные:
1.
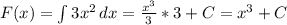
Подставляем в первообразную границы интегрирования:

2.
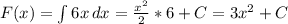
Подставляем в первообразную границы интегрирования:
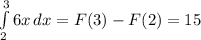
3.

Подставляем в первообразную границы интегрирования:
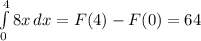
4.
Производим ровно те же операции, что и до этого, так как требуется найти путь у параболы ветвями вверх => интеграл не будет отрицательным.
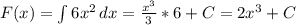
Подставляем в первообразную границы интегрирования:
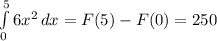
5.
Находим первообразную заданной функции:

Ограничивающие прямые - те же границы интегрирования:

2в 6б 180 руб
5в 6б 270 руб
Второй комплект больше на 3 верблюда и на 90 рублей. Значит 1 верблюд стоит 90/3=30 руб.
Значит 2 верблюда стоят 2*30=60 руб.
6 баранов стоит 180- 60 =120 руб.
120/6=20 руб стоит баран.