(-∞;-6]∪(5;+∞)
Пошаговое объяснение:
В первом неравенстве надо просто проставить знаки. Отметим на числовой прямой точки -6,1,4, т.е. решения этих скобок. Т.к. у нас во всех скобках перед x стоит положительный коэффициент, все скобки линейные (т.е. в первой степени), то знаки расставляются справа налево, начиная с "+". Т.е. (x-1)(x-4)(x+6)≥) выполняется при x∈[-6;1]∪[4;+∞]
Чтобы решить второе неравенство, решим соответствующее квадратное уравнение: x^2-25=0
x=±5
Также расставляем знаки и получаем, что выполняется при x∈(-∞;-5)∪(5;+∞)
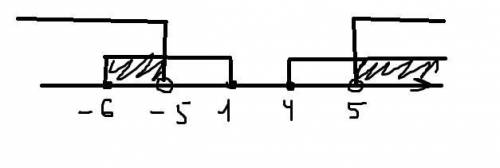
Теперь нужно найти пересечение этих промежутков. Опять строим числовую прямую и будем работать методом прямоугольников (картинка прилагается)
Таким образом, конечный ответ это (-∞;-6]∪(5;+∞)
В равнобедренном треугольнике, высота, опущенная из вершины к основанию является медианой и биссектрисой.
Проведем высоту ВH, разделив первоначальный треугольник пополам.
Такая "половина" есть Треугольник ABH - прямоугольный. Рассмотрим его и найдем все стороны.
AB = 5
угол ABH=60 градусов
угол BAH= 30градусов
По теореме, сторона прямоуг треугольника, лежащая напротив угла 30 градусов, равна половине гипотенузы. Гипотенуза рана 5, значит BH равно 2,5.
По теореме Пифагора найдем AH.
Получаем AH=2,5 * Корень(3).
AH это половина AС, тогда АС будет 5*Корень(3).
Площадь всего треугольника АВС будет равна
1/2*основание*Высота
1/2*5*Корень(3)*2,5=6,25*Корень(3) Площадь треугольника ABC
С другой стороны Площадь треугольника можно посчитать по другой формуле, через радиус описанной окружности:
S=(abc)/4R
S= (5*5*5*Корень(3))/4R=(125*Корень(3))/4R
(125*Корень(3))/4R=6,25*Корень(3) -- справа рассчитанная ранее Площадь.
Решаем уравнение:
R=5.