t1^2+2*t1*t2-t2^2=0
Сразу приметим решение: t1=t2=0 ,чтобы не забыть о нем в дальнейшем. (Как я предполагаю, данная задача , это приложение к какой то задаче о времени , поэтому данное решение не представляет для нас какого то интереса. Если я неправ ,то поправьте меня)
Теперь можно поделить обе части уравнения на t1^2
1+2*(t2/t1) -(t2/t1)^2=0
Делаем замену: t2/t1=x
1+2x-x^2=0
x^2-2x-1=0
(x-1)^2=2
x12=1+-√2
Значение : 1-√2<0 , такое значение нас не устраивает в силу положительности времен : t1 и t2
Вывод:
t2=t1*(1+√2)
Пошаговое объяснение:
1) (18-8х)-(2х-6)=13+х
18 - 8х -2х +6 -х = 13
-11х = 13-24
-11х = -11
х =1
2)(х+2)-(5-2х)=15-(3х+8)
х +2 - 5 + 2х = 15 - 3х - 8
6х = 10
3х = 5
х = 5/3
х =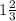
3) (5у+3)-(2у-4)=(у-2)-(у+3)
5у + 3 - 2у + 4 = у -2 - у -3
3у = - 12
у = -4