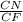⇒СF = 
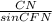⇒ CF = 5/sin∠60°CF = 5/(√3/2)CF = 10/√3 cмCF = BD (cм пункт №3)⇒ BD = 10/√3 cм5. Рассмотрим трапецию ABCDЗа формулой S = 
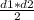*sina где а = угол между диагоналями d1 и d2За условием диагонали перпендикулярны⇒ S =(BD*AC/2)* sin∠90°S =10*(10/√3)/2S =50/√3 cм²Так же площадь можно найти через среднюю линию и высоту за формулой:S = m · h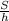⇒m = 
m =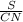 
m= (50/√3)/5m= 10/√3 cмответ: m= 10/√3 cмхух это было оч. долго...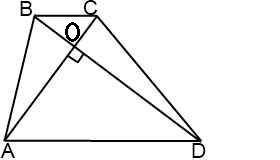 
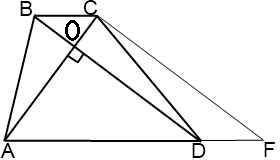
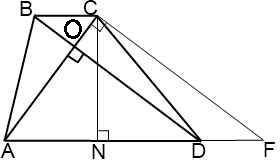
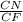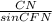⇒СF = ⇒ CF = 5/sin∠60°CF = 5/(√3/2)CF = 10/√3 cмCF = BD (cм пункт №3)⇒ BD = 10/√3 cм5. Рассмотрим трапецию ABCDЗа формулой S = 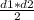*sina где а = угол между диагоналями d1 и d2За условием диагонали перпендикулярны⇒ S =(BD*AC/2)* sin∠90°S =10*(10/√3)/2S =50/√3 cм²Так же площадь можно найти через среднюю линию и высоту за формулой:S = m · h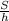⇒m = m = 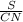m= (50/√3)/5m= 10/√3 cмответ: m= 10/√3 cмхух это было оч. долго...
Лёгкая атлетика
Джесси Оуэнс
Jesse Owens3.jpg
Джесси Оуэнс на Играх 1936 года
Общая информация
Полное имя Джеймс Кливленд Оуэнс
Дата и место рождения 12 сентября 1913[1][2][3]
Оуквилль, штат Алабама, США
Дата и место смерти 31 марта 1980[1][2][3] (66 лет)
Тусон, Аризона, США[4]
Гражданство
Flag of the United States.svg США
Рост 180 см
Вес 75 кг
IAAF 270934
Личные рекорды
100 м 10,2[5] (1936) WR*
200 м 20,3[5] (1935) WR*
Длина 8,13[5] (1935) WR*
Международные медали
Олимпийские игры
Золото Берлин 1936 100 м
Золото Берлин 1936 200 м
Золото Берлин 1936 эстафета 4×100 м
Золото Берлин 1936 длина
Государственные награды
Presidential Medal of Freedom (ribbon).png
Commons-logo.svg Джесси Оуэнс на Викискладе
Джеймс Кливленд (Джесси) Оуэнс (англ. James Cleveland «Jesse» Owens; 12 сентября 1913, Оуквилль, Алабама — 31 марта 1980, Тусон, Аризона) — американский легкоатлет, специализировавшийся на спринтерском беге и прыжках в длину.
На Олимпийских играх 1936 года стал четырёхкратным олимпийским чемпионом, выиграв дистанции 100 и 200 метров, эстафету 4×100 метров (с мировым рекордом) и прыжки в длину. Впоследствии это достижение смог повторить только Карл Льюис на Играх 1984 года. Победы афроамериканца Оуэнса на Олимпиаде в Берлине были символическим ударом по расовой теории нацистской Германии[источник не указан 165 дней].
Содержание
1 Биография
2 Спортивная карьера
2.1 Олимпийские игры 1936
3 Оуэнс в филателии
4 Память
5 Примечания
Биография
Джесси Оуэнс родился в семье Генри Кливленда Оуэнса и Мэри Эммы Фицжеральд и был младшим из 10 детей: семерых братьев и трёх сестёр. Когда ему было 9 лет, из-за расовой сегрегации семья была вынуждена переехать в Кливленд (штат Огайо). Его новый школьный учитель, чтобы вызвать его к доске, прибегал к сокращению «J. C.», но благодаря сильному южному акценту, получалось «Джесси». Прозвище впоследствии перешло в официальное имя.
Подростком перепробовал много профессий: работал поставщиком в бакалейную лавку, грузчиком, открыл мастерскую по ремонту обуви.
Со своей будущей женой Мини Руф Соломон познакомился ещё в средней школе Фармунт, что в Кливленде, когда ему было 15 лет, а ей — 13 лет. Первая дочь, Глория, родилась у них в 1932 году. Поженились они в 1935 году, и этот брак дал им ещё двух дочерей: Марлен (1939) и Беверли (1940). Брак этот продолжался до самой смерти.