Если m=1, то m является полным квадратом (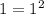
), поэтому этот случай можно не рассматривать.
Пусть m>1 не является полным квадратом, тогда в разложении m на простые множители (существование такого разложения гарантируется основной теоремой арифметики)
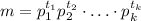
хотя бы один показатель является нечетным числом. Не теряя общности, можно предположить, что это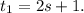 
По условию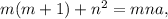 
где a - целое число. Разделим это равенство на m:
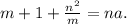
Поскольку m+1 и na - целые числа,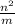 
является целым числом, то есть 
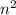делится на m, откуда 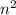делится на 
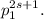Отсюда следует, что n делится на 
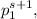следовательно 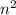делится на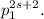 
Теперь мы уже на финише. Из последнего рассуждения следует, что 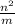делится на 
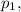na, естественно, делится на 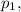но (m+1) ну никак не может делиться на 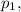поскольку соседние натуральные числа взаимно просты (а m делится на 
).
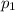Полученное противоречие доказывает, что m обязано быть полным квадратом.
Раздели его на 2 равные части.какие доли отрезка получились.
8:2=4 см в каждой из двух частей отрезка.
4/8=1/2 и 4/8=1/2 - доли отрезка получились.
Сколько их?
2 доли.
Раздели каждую половину ещё на 2 равные части.
4:2=2 см в каждой из четырех частей отрезка.
2/8=1/4; 2/8=1/4; 2/8=1/4; 2/8=1/4 - доли целого отрезка.
Сколько их в целом отрезке.
4 доли в целом отрезке.
Сколько четвёртых долей отрезка в его половине?
Две четвертых доли в половине отрезка.
Раздели каждую четвёртую долю отрезка на 2 равные части. Какие доли целого отрезка получились?
2:2=1 см в каждой из восьми частей отрезка
1/8; 1/8; 1/8; 1/8; 1/8; 1/8; 1/8; 1/8 -доли целого отрезка
Сколько восьмых долей в трёх четвёртых отрезка?
6/8 долей в трех четвертях целого отрезка.
Чертеж:
о|||||||o