ответ:
Пошаговое объяснение:
Из условия следует, что уравнение f(x)-x=0 не имеет решений. Поскольку f(x)-x - непрерывная функция, то она либо всюду положительна, либо всюду отрицательна, иначе она бы в некоторой точке принимала значение 0 (по теореме о промежуточном значении). Пусть f(x)-x всюду положительна. Это значит, что для любого x выполнено неравенство f(x)>x. Пусть f(x)=y. Тогда f(f(x))=f(y)>y=f(x)>x. Таким образом, при любом x f(f(x))-x>0, т.е. уравнение f(f(x))=x не имеет корней. Аналогичным образом, показываем, что уравнение f(f(x))=x не имеет корней и в том случае, когда для любого x выполнено неравенство f(x)<x.
Пусть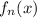 
означает 
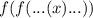, где 
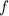применена 
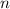раз.
Поскольку 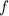многочлен, то у него есть значение в любой точке. (*)
Докажем утверждение по индукции.
База: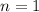 
- это то, что дано по условию.
Переход:
Пусть для некоторого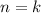 
верно; Докажем, что из этого следует справедливость утверждения и для 
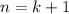; Действительно, по предположению индукции множество решений уравнения 
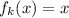совпадает с 
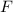; Возьмем 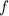от обеих частей (благодаря (*) мы можем это сделать): 
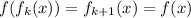; Но если сделать замену 
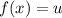, получим 
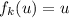; А множество решений этого уравнения лежит в 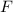; Предположим, что есть некоторый элемент 
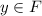, такой, что для него не найдется 
, чтобы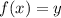 
; Тогда 
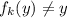, но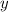 
лежит в 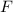, противоречие. Это завершает переход.
896
Пошаговое объяснение:
510---15---20--25--30--35--40--45
50--55--60--65--70--75--80--85--90--95
Всего 19 чисел
950 - сумма всех чисел
Из 19 чисел можно составить 9 пар (2*9=18) и одно число останется не парным
Вывод 1:
1.1) после первого круга будет 9 новых чисел и "одно старое непарное".
итого: 10 чисел
1.2) сумма чисел 950-3*9=923 (т.к. от каждой пары отняли 3 от первоночальной суммы)
Из 10 чисел можно составить 5 пар
Вывод 2:
2.1) после второго круга будет 5 новых чисел
2.2) сумма чисел 923-3*5=908 (т.к. от каждой пары отняли 3 от первоночальной суммы)
Из 5 чисел можно составить 2 пар (2*2=4) и одно число останется не парным
Вывод 3:
3.1) после третьего круга будет 2 новых числа и "одно старое непарное".
итого: 3 числа
3.2) сумма чисел 908-3*2=902 (т.к. от каждой пары отняли 3 от первоночальной суммы)
Из 3 чисел можно составить 1 пару (1*2=2) и одно число останется не парным
Вывод 4:
4.1) после четвертого круга будет 1 новое число и "одно старое непарное".
итого: 2 числа
4.2) сумма чисел 902-3*1=899 (т.к. от каждой пары отняли 3 от первоночальной суммы)
Из 2 чисел можно составить 1 пару
Вывод 5:
5.1) после пятого круга будет 1 новое число
2.2) число 899-3*1=896 (т.к. от каждой пары отняли 3 от первоночальной суммы)
ответ: 896