Пусть мастер изготавливает х деталей в день. Тогда все задание он выполнит за: 240 : х дней.
Если же он будет в день изготавливать х + 6 деталей, то на исполнение заказа ему потребуется: 240 : (х + 6) дней.
Тогда:
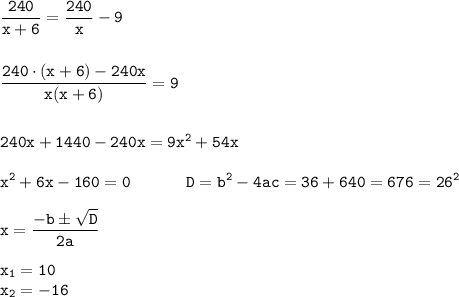
Так как, по условию, х ∈ N, то х₂ не удовлетворяет условию задачи.
Таким образом, если мастер будет изготавливать 10 деталей в день, то заказ в 240 деталей он выполнит за 24 дня.
Если же он увеличит число выпускаемых деталей на 6, то их станет 16 в день, и весь заказ мастер выполнит за: 240 : 16 = 15 дней, то есть, на 9 дней раньше.
--------------------------
ответ: 10 дет. в день в обычном темпе и 16 дет. в день в ускоренном.
9 попыток
Пошаговое объяснение:
АБСД - 4х значный пароль
А может быть или 0 или 1 или 2 - три варианта
Б может быть или 1 или 2 или 0 - три варианта
С может быть или 1 или 2 или 0 - три варианта
Д может быть или 1 или 2 или 0 - три варианта
3*3*3*3=81 - количество 4-хзначных чисел, которые можно составить из чисел 1,2,0
Например: 0000, 0222, 1200
Известно, что каждая попытка позволяет проверить правильность не только самого номера, но и всех номеров, отличающихся от введённого ровно в одной позиции
0000--0001--0002--0010--0020--0100--0200--1000--2000
0222--0220--0221--0202--0212--0022--0122--1222--2222
1200--1201--1202--1210--1220--1000--1100--0200--2200
Вывод 1: из каждого номера можно получить 8 номеров, отличающихся от начального ровно в одной позиции
Значит одним номером (паролем), Эдик может проверить 9 номеров
Вывод 2:
81 : 9 = 9 - номеров должен ввести Эдик, что бы проверить все 81 пароли
Определим один вариант паролей, которые может ввести Эдик (9штук)
1) напишем все варианты паролей - 81 номеров
2) сгруппируем все номера по двум последним числам (-00-,-01-,-02-,-10-,-11-,-12-,-20-,-21-,-22-) получилось 9 групп
3) в каждой группе, разместим номера в порядке возрастания
-------- смотрите фото --------
4) из полученной таблице выберите числа
5) проверим выбранные номера и номера отличающиеся от них в одной позиции на "повторки" (повторов быть не должно)
У нас получились номера (смотрите фото)
1200--0101--2002--0010--2211--1112--2120--1021--0222
Если прописать эти числа и числа, отличающихся от них в одной позиции, получится 81 пароль (повторов нет). Смотри фото)))
Как видно из таблицы (фото), мы взяли по одному числу из каждой группы (строки) и каждого столбца
Вывод: с таблицы можно найти все 9 вариантов паролей (по 9 штук в каждой). И в каждом варианте одно число будет оканчиваться на -00-, второе на -01-, третье на -02-, четвертое на -10-, пятое -11-, шестое на -12-, седьмое на -20-, восьмое на -21-, девятое на -22-.
ответ: 9 попыток