• формула корней квадратного уравнения:
2
b d
x
a
− ±
=
, где
2 d b ac = − 4 .
• если квадратный трехчлен 2 ax bx c + + имеет два корня x1 и x 2 , то
( )( ) 2 ax bx c a x x x x + += − − 1 2 ;
если квадратный трехчлен 2 ax bx c + + имеет единственный корень x 0 , то
( ) 2 2 ax bx c a x x + += − 0 .
• формула n -го члена арифметической прогрессии ( ) a n , первый член которой
равен a1 и разность равна d :
a a dn n =+ − 1 ( ) 1 .
• формула суммы первых n членов арифметической прогрессии:
( ) 1
2
n
n
a an
s
+
=
.
• формула n -го члена прогрессии bn , первый член которой
равен b1, а знаменатель равен q :
1
1
n b bq n − = ⋅
• формула суммы первых n членов прогрессии:
( ) 1 1
1
n
n
q b
s
q
−
=
−
.
таблица квадратов двузначных чисел
единицы
0 1 2 3 4 5 6 7 8 9
1 100 121 144 169 196 225 256 289 324 361
2 400 441 484 529 576 625 676 729 784 841
3 900 961 1024 1089 1156 1225 1296 1369 1444 1521
4 1600 1681 1764 1849 1936 2025 2116 2209 2304 2401
5 2500 2601 2704 2809 2916 3025 3136 3249 3364 3481
6 3600 3721 3844 3969 4096 4225 4356 4489 4624 4761
7 4900 5041 5184 5329 5476 5625 5776 5929 6084 6241
8 6400 6561 6724 6889 7056 7225 7396 7569 7744 7921
десятки
9 8100 8281 8464 8649 8836 9025 9216 9409 9604 98
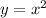 на одну единицу вверх вдоль (параллелно) оси OY. График "поднимается" .
на одну единицу вверх вдоль (параллелно) оси OY. График "поднимается" .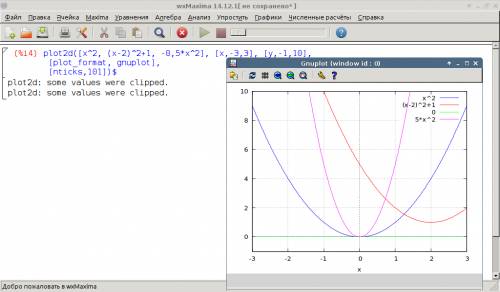
Объяснение:
1) Коэффициент при старшей степени (x^2) положительный, соответственно, ветви параболы направлены вверх
2) Чтобы уравнение имело 2 различных корня, дискриминант должен быть больше 0 (если дискриминант равен 0, то ответом являются 2 одинаковых корня; если дискриминант меньше 0, то корней на множестве действительных чисел нет)
D=b^2-4ac=(a-5)^2-4*1*9=a^2-10a+25-36=a^2-10a-11
a^2-10a-11>0
Найдем нули:
a^2-10a-11=0
a1=-1
a2=11
3) Выражение можно разложить на множители по формуле a(x-x1)(x-x2)
1*(a+1)(a-11)
(a+1)(a-11)>0
Расставим на числовой оси эти точки (выколотые) и знаки, получим ответ
a∈(-∝;-1)U(11;+∝)
ответ: a∈(-∝;-1)U(11;+∝)