![\sqrt{1-\frac{2x-1}{3}}+\sqrt{2x-\frac{x}{3}-\frac{2}{15}}=\sqrt{\frac{3-2x+1}{3}}+\sqrt{\frac{30x-5x-2}{15}}=\sqrt{\frac{4-2x}{3}}+\sqrt{\frac{25x-2}{15}}\\\\\\O.O.\; \; \left \{ {{\frac{4-2x}{3}\geq 0} \atop {\frac{25x-2}{15}\geq 0}} \right.\; \; \left \{ {{4-2x\geq 0} \atop {25x-2\geq 0}} \right.\; \; \left \{ {{x\leq 2} \atop {x\geq 0,08}} \right.\; \; \Rightarrow \; \; \; x\in [\, 0,08\; ;\; 2\; ]](/tpl/images/1009/9028/d3011.png)
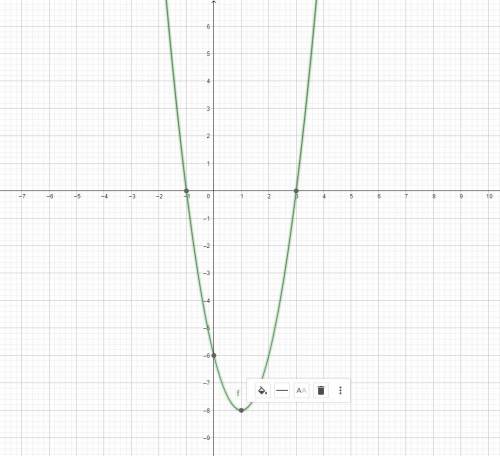
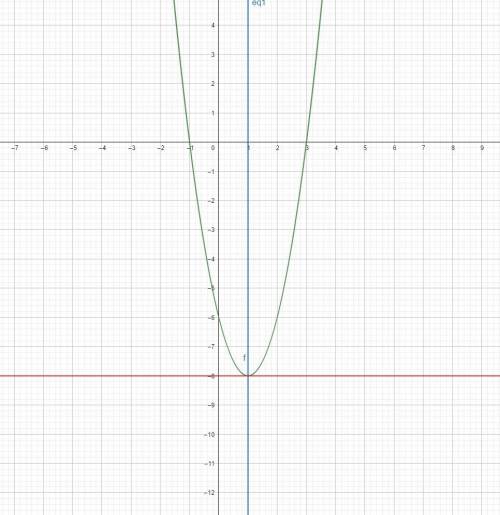
Я прикрепил фото того, как выглядит график. А сейчас разберемся как его строить.
Для начала давай раскроем скобки:
y = (2x - 6)(x + 1) //внесли двойку
y = x*(2x - 6) + (2x - 6) //раскрыли вторую скобку
y = 2x^2 - 6x + 2x - 6
y = 2x^2 - 4x - 6
Теперь можно решать по разному. Если хочешь напишу ещё
А пока воспользуемся самым действенным
Примем x0 и y0 за координаты вершины параболы.
Тогд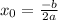а 
, а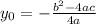 
(вторую формулу если что можно не запоминать, можешь просто подставить в уравнение полученное x0)
И так
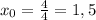
Значит
Теперь может просто подставлять значения. Но в данном случае можешь схитрить.
Так как изначальное уравнение выглядело как y = 2(x - 3)(x + 1), то если присмотреться, то можно заметить, что эта парабола пересекает ось x в точках 3 и -1. Но самое интересное это коэффициент 2. Ты можешь просто квадраты x умножать на два и получать желанную точку. После просмотра второй картинки, мои слова станут более понятны
Биномиальное распределение стремится к нормальному при больших n
По условию
р = 0.9
соответственно
q = 1- p = 0.1
Математическое ожидание
М= np= 1000 * 0.9 = 900
Дисперсия
D= npq = 1000*0.9*0.1= 90
Сигма = √D= 3√10 = ~9.5
Мы рассматриваем интервал от центра распределения 900 до 940 - это больше чем четыре сигмы.
В этом случае в табличку нормального распределения можно даже не заглядывать, хвостик за четыремя сигмами очень малюсенький, пятый знак после запятой.
Половина всей выборки до 900 , половина после.
ответ
Вероятность равна ~0.5
