y = 2x^3 - 3x^2 - 12x + 1 – это кубическая функция, проверим имеет ли она максимумы и минимумы, для этого найдем производную и приравняв у нулю, найдем промежутки возрастания и убывания. Если они имеются.
y = (2x^3 - 3x^2 - 12x + 1)’ = 6x^2 – 6x – 12;
6x^2 – 6x – 12 = 0;
x^2 – x – 2 = 0;
D = b^2 – 4ac;
D = (- 1)^2 – 4 * 1 * (- 2) = 1 + 8 = 9; √D = 3;
x = (- b ± √D)/(2a);
x1 = (1 + 3)/2 = 4/2 = 2;
x2 = (1 - 3)/2 = - 2/2 = - 1
Точки с абсциссами (- 1) и 2 – являются экстремумами, но ни одна из них не принадлежит промежутку [4; 5]. Значит наибольшее значение функции будет либо в точке 4, либо в точке 5.
y(4) = 2 * 4^3 – 3 * 4^2 – 12 * 4 + 1 = 128 – 48 – 48 + 1 = 129 – 96 = 33
y(5) = 2 * 5^3 – 3 * 5^2 – 12 * 5 + 1 = 250 – 75 – 60 + 1 = 251 – 135 = 116 – это наибольшее значение функции на интервале [4; 5].
ответ. max [4; 5] y = у(5) = 116.
Р = 28 см.
Объяснение:
По условию смежные стороны прямоугольника относятся как 3:4.
Обозначим одну часть через x.
Тогда ширина прямоугольника будет равна 3х, т.к. осоставляет 3 таких части, а длина прямоугольника будет равна 4х, т.к. оставляет 4 таких части.
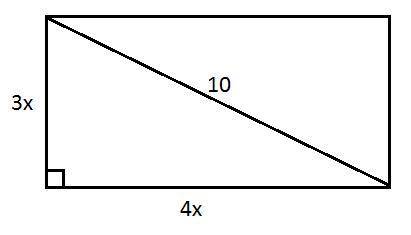
Диагональ в прямоугольнике с двумя смежными сторонами образует прямоугольный треугольник (см. рисунок). Диагональ равна 10 см.
Воспользуемся теоремой Пифагора и составим уравнение.
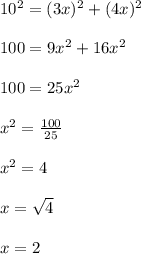
Ширина прямоугольника: 3х = 3·2 = 6 (см).
Длина прямоугольника: 4х = 4·2 = 8 (см).
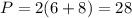 (см)
(см)
4) ( с-5) вверху 2
5) (2m+1) вверху 2
6) (4- с) вверху 2