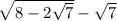
тут мы иммем дело с разницей квадрата под корнем. его надо уметь видеть.
= 
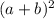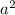+ 2ab +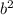 
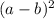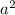= - 2ab +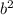
в данном случе второе(минус перед два корней из семи).
И так 2√7 - в данном случае это у нас 2ab.
8 - это сума а в квадрате и б в квадрате.
то есть:
8 = +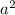
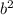
2ab = 2√7
ab = √7
То есть нам нужно методом подбора подобрать такие числа, чтобы их сумма в квадрате была 8, а при умножении они давали корень из семи. (тут метод подбора ничего более просто нужны тренировки и практика для этого).
Я подобрала:
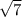и 1. И в правду, 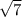* 1 =[/tex]\sqrt{7}[/tex]
и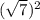 
+ 
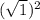= 7 + 1 = 8
то есть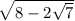 
= 
= |
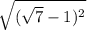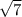- 1| (по модулю, модуль убираем, ибо 
|
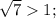То есть:
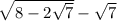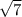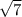= - 1 - = -1.
ответ: -1.
В решении.
Объяснение:
Дана функция у=√х:
а) График которой проходит через точку с координатами А(а; 2√6). Найдите значение а.
Нужно в уравнение подставить известные значения х и у (координаты точки А):
2√6 = √а
(2√6)² = (√а)²
4*6 = а
а=24;
b) Если х∈[0; 16], то какие значения будет принимать данная функция?
у= √х
у=√0=0;
у=√16=4;
При х∈ [0; 16] у∈ [0; 4].
с) y∈ [13; 19]. Найдите значение аргумента.
13 = √х
(13)² = (√х)²
х=169;
19 = √х
(19)² = (√х)²
х=361;
При х∈ [169; 361] y∈ [13; 19].
d) Найдите при каких х выполняется неравенство у ≤ 3.
√х <= 3
(√х)² <= (3)²
х <= 9;
Неравенство у ≤ 3 выполняется при х <= 9.