Производная по определению - предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует.
Δy = f(x+Δx) - f(x) = √(1+2(x+Δx)) - √(1+2x) = √(1+2x+2Δx) - √(1+2x)
Преобразуем выражение, домножив числитель и знаменатель на сопряженное выражение:
(√(1+2x+2Δx) - √(1+2x))(√(1+2x+2Δx) + √(1+2x))/(√(1+2x+2Δx) + √(1+2x)) = (1+2x+2Δx - 1 -2x)/(√(1+2x+2Δx) + √(1+2x))= (2Δx)/(√(1+2x+2Δx) + √(1+2x))
Δy/Δx = 2/(√(1+2x+2Δx) + √(1+2x))
limΔx->0 (2/(√(1+2x+2Δx) + √(1+2x)) = 2/(√(1+2x) + √(1+2x)) = 2/(2√(1+2x) = 1/√(1+2x)
ответ: y' = 1/√(1+2x)
Не все так просто:))). Сначала нам нужно обязательно, чтобы появилась карточка с цифрой "3". Это, конечно 1/4 . Потом при условии, что эта карточка уже выбрана, нам нужно получить карточку с цифрой "1". Так как остались всего 3 карточки, то вероятность этого события уже больше 1/3. Затем нам нужно, при условии уже сложившихся событий, получить карточку "5". Это 1/2. А потом уже само собой выйдет карточка "7" с вероятностью 1/1.
По формуле условной вероятности все эти вероятности нужно перемножить
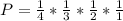
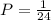
x^2+2ax+2a-1=0
найдём дискриминант
D=(2a)^2-4*1*(2a-1)=4aa-8a+4=(2a-2)^2
нас интересует только когда существует два корня уравнения ,
а значит D>0 , это выполняется когда a не равно 1
тогда первый корень будет равен
(-2a+D^(1/2)):2=(-2a+2a-2):2=-1
второй корень уравнения равен
(-2а-D(1/2)):2=(-2a-(2a-2)):2=(-4a+2):2=-2a+1
соотношение корней равно 3:1
(-1):(-2a+1)=3:1
2a-1=1/3
2a=1+1/3
2a=4/3
a=2/3 - это решение проверим, подставив а=2/3,
получаем уравнение:
x^2+(4/3)x +1/3=0
корни этого уравнения равны -1 и -1/3
(-2а+1):(-1)=3:1
2а-1=3
2а=4
а=2
проверим решение, подставив а=2
получим уравнение
x^2+4x+3=0
корни этого уравнения -1 и -3
ответ: при а=2 и а=2/3