Поступим следующим образом: косинус перенесем влево с противоположным знаком и обе части разделим на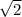 
(это же самое, что умножить на дробь 
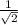) Имеем:
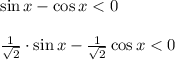
Заметим, что
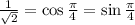
Если переписать неравенство в следующем виде -
,
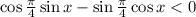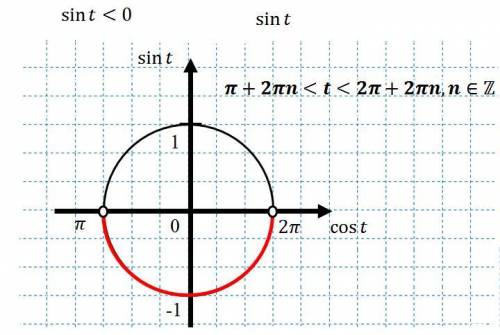
то легко можно заметить в левой части формулу синуса разности аргументов. Окончательно имеем:
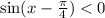
Сделаем замену: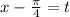 
. Таким образом мы свели исходное неравенство к наипростейшему вида 
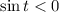. Решим его при числовой окружности (вложение). Окончательно имеем: 
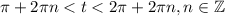. Возвращаемся к обратной замене: 
.
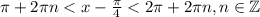Ко всем 3-ем частям неравенства прибавляем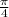 
и получаем окончательный ответ: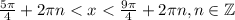 
ОТВЕТ: .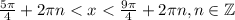
Уравнение прямой, отсекающей от первого координатного угла треугольник, имеет вид y=kx+b . Этот треугольник прямоугольный и его площадь равна половине произведения катетов.
Так как точка А(1;2) принадлежит этой прямой,то подставив координаты точки А(1;2) в это уравнение получим
Уравнение прямой теперь будет выглядеть так: 
.
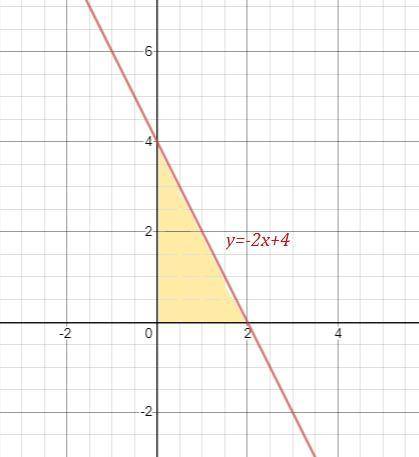
Найдём точки пересечения этой прямой с осями координат:
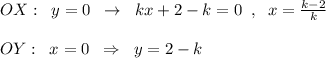
Длины отрезков, отсекаемых прямой y=kx+2-k на координатных осях, равны (2-k) на оси ОУ и (k-2)/k на оси ОХ. Эти отрезки и есть катеты прямоугольного треугольника. Вычислим его площадь:
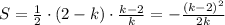
Найдём минимум это функции S(k).
Точка минимума: 
, так как при переходе через k= -2 производная меняет знак с минуса на плюс.
При k= -2 уравнение искомой прямой будет
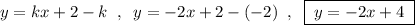
ответ: k= -2 .
Объяснение:
1) Разложить. Раскрыть скобки:
2) Раскрыть скобки:
3) Вычислить сумму:
4) Убрать равные слагаемые:
5) Поменять стороны местами:
6) Разделить обе части уравнения на 4: