И так распишем модуль по определению.
Так программа не позволяет записывать большие уравнения буду делать по частям, а потом всё объединять.
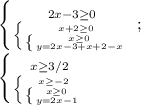
1. x≥3/2, y=2x-1
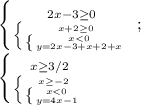
У этой системы нет пересечения.
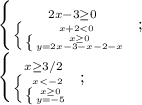
У этой системы нет пересечения.
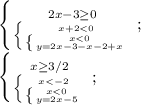
У этой системы нет пересечения.
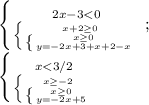
2. 0≤x<3/2, y=-2x+5
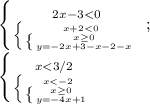
У этой системы нет пересечения.
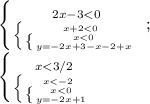
3. x<-2, y=-2x+1
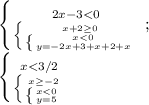
4. -2≤x<0, y=5
Я перебрал все возможные случаи раскрытия модулей теперь посмотрим прерываются ли эти графики.
1. x≥3/2, y=2x-1;
2. 0≤x<3/2, y=-2x+5;
3. x<-2, y=-2x+1;
4. -2≤x<0, y=5.
f1(3/2)=3*2/2-1=2 и f2(3/2)=-2*3/2+5= -3+5=2 Эти концы сходятся.
f2(0)= -2*0+5=5 и f4(0)=5 сходятся
f4(-2)=5 и f3(-2)= -2*(-2)+1=4+1=5 сходятся.
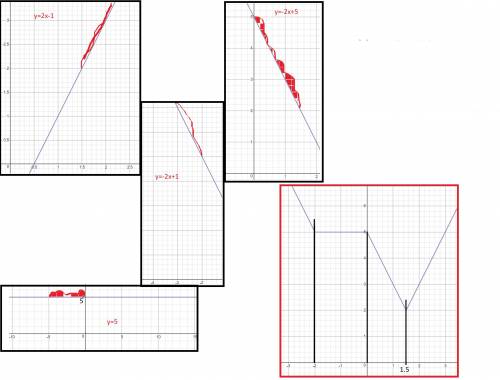
Далее рисуем каждый график отдельно отмечай необходимый нам интервал и переносим всё на один график. См. график внизу
так как не требуется найти конкретные корни. а только их количество. найду их приблизительные значения
так как функция справа и слева четная, то графики правой и левой части симметричны относительно оси у
поэтому рассмотрю решение для положительного х, такое же решение с противоположным знаком-тоже будет корнем
-x^2+4x=-√(2x)
-x^2+4x+√(2x)=0
√(2x)=x^2-4x
все в квадрат
2x=x^2(x-4)^2
x^2(x-4)^2-2x=0
x(x(x-4)^2-2)=0
x1=0
приравниваю скобку к 0
2=x(x-4)^2
решение уравнения третьей степени в школе не особо любят, поэтому укажу его приблизительное значение
x2≈4.6
значит решение x3=-4.6- тоже решение
Тогда выходит у заданного уравнения три решения