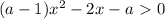
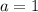Алгебра: Знайти b10 , якщо b1=√2 , q=√2

Знайти b10 , якщо b1=√2 , q=√2

👇

Увидеть ответ

Ответ:

ЕvilСookie

19.09.2022

b10=32

Объяснение:

4,7(10 оценок)

Открыть все ответы

Ответ:

Bananchik26

19.09.2022

$(a-1)x^2-2x-a\ \textgreater \ 0$
Если a=1

, то получим линейное неравенство: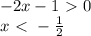
$-2x-1\ \textgreater \ 0
\\\
x\ \textless \ - \frac{1}{2}$
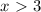Полученный промежуток не включает в себя заданыый $x\ \textgreater \ 3$ .
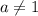Рассматриваем случай, когда $a \neq 1$ - имеем квадратное неравенство.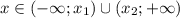
Заданное неравенство ">0", в зависимости от знака старшего коэффициента общие решения неравенства можно записать в виде:
- если старший коэффициент больше 0: $x\in(-\infty;x_1)\cup(x_2;+\infty)$
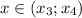
- если старший коэффициент меньше 0: $x\in (x_3;x_4)$
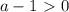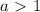
Вывод: необходимо рассмотреть случай с положительным старшим коэффициентом: $a-1\ \textgreater \ 0$ , тогда $a\ \textgreater \ 1$
Решаем неравенство. Приравниваем левую часть к нулю:
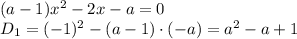
$(a-1)x^2-2x-a=0
\\\
D_1=(-1)^2-(a-1)\cdot(-a)=a^2-a+1$
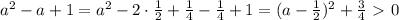
Получившийся дискриминант всегда больше 0, т.к. $a^2-a+1=a^2-2\cdot \frac{1}{2} + \frac{1}{4} - \frac{1}{4} +1=(a- \frac{1}{2} )^2+ \frac{3}{4}\ \textgreater \ 0
$
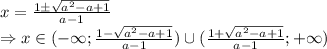
$x= \frac{1\pm \sqrt{a^2-a+1} }{a-1} 
\\\
\Rightarrow x\in(-\infty; \frac{1-\sqrt{a^2-a+1} }{a-1} )\cup( \frac{1+\sqrt{a^2-a+1} }{a-1} ;+\infty)$
Чтобы получившийся ответ включал интервал х>3, необходимо потребовать выполнение следующего условия:
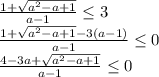
$\frac{1+\sqrt{a^2-a+1} }{a-1} \leq 3
\\\
 \frac{1+\sqrt{a^2-a+1} -3(a-1)}{a-1} \leq 0
\\\
 \frac{4-3a+\sqrt{a^2-a+1} }{a-1} \leq 0$
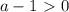Так как в рассматриваемом случае $a-1\ \textgreater \ 0$ , то можно перейти к следующему неравенству:
$4-3a+\sqrt{a^2-a+1} \leq 0
\\\
\sqrt{a^2-a+1} \leq 3a-4
\\\
\begin{cases} a^2-a+1 \leq (3a-4)^2 \\ 3a-4\ \textgreater \ 0 \right \end{cases}
\\\
\begin{cases} a^2-a+1 \leq 9a^2-24a+16 \\ 3a\ \textgreater \ 4 \right \end{cases}
\\\
\begin{cases} 8a^2-23a+15 \geq 0 \\ a\ \textgreater \ \frac{4}{3} \right \end{cases}
\\\
\begin{cases} a\in(-\infty;1]\cup[ \frac{15}{8} ;+\infty) \\ a\ \textgreater \ \frac{4}{3} \right \end{cases}$
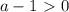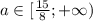
Итоговое решение с учетом рассматриваемого ограничения $a-1\ \textgreater \ 0$ : $a\in[ \frac{15}{8} ;+\infty)$
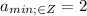
Искомое минимальное целое значение $a_{min; \in Z}=2$
ответ: 2

4,7(51 оценок)

Ответ:

красотка368

19.09.2022

Объяснение:

потому что у нас есть равенство, а равенство можно умножать( обе части) на одно и то же отличное от нуля число, для удобства умножили на 6, тогда в левой части знаменатель сократился, а в правой 0*6 все равно 0.

Второй вариант объяснения. Мы знаем, что знаменатель дроби никогда не равен нулю, тогда при равенстве дроби к нулю мы должны записать систему, где числитель равен нулю, а знаменатель не равен нулю, в нашем случае, в знаменателе константа, т.е. такое выражение которое не зависит от переменной( нет букв)). А значит оно никогда не равно нулю, и нашу систему можно переписать как одно первое уравнение, а именно, числитель равен нулю. Надеюсь

4,7(73 оценок)

Это интересно:

Здоровье

12.11.2020

Молочница: Причины, проявления и лечение в домашних условиях...

Дом-и-сад

10.09.2020

Как установить в доме камеры наблюдения для системы безопасности...

Кулинария-и-гостеприимство

23.06.2020

Как заварить Кунг фу чай - лучший способ насладиться вкусом восточного чая...

Кулинария-и-гостеприимство