Если ещё не изучено понятие производной, то решение может быть таким:
1. -2;
2. 3.
Объяснение:
1.Sn=6n-n^2
a1 = S1 = 6•1 - 1^2 = 5;
a1+a2 = S2 = 6•2 - 2^2 = 12 - 4 = 8;
a2 = S2 - S1 = 8 - 5 = 3.
Найдём d:
d = a2 - a3 = 3 - 5 = -2.
2. Sn=6n-n^2
Рассмотрим квадратичную функцию
у = 6х - х^2.
Графиком функции является парабола
у = - х^2 + 6х
Ветви параболы направлены вниз, своего наибольшего значения функция достигает в вершине параболы. Найдём её координаты:
х вершины = -b/(2a) = -6/(-2) = 3.
y вершины = - 3^2 +6•3 = -9+18 = 9.
Наибольшего значения 9 функция у = - х^2 + 6х достигает при х = 3.
Так как 3 - натуральное число, то и наша функция Sn=6n-n^2, определённая только для натуральных n, достигает наибольшего значения 9 при n = 3.
Необходимо взять три первых члена прогрессии, чтобы их сумма была наибольшей и равной 9.
ответить на второй вопрос можно и по-прежнему другому:
Sn=6n-n^2
- n^2 + 6n = - (n^2 - 6n) = - (n^2 -2•n•3 + 9 - 9) = - ((n-3)^2 -9) = - (n-3)^2 + 9.
Так как слагаемое 9 постоянно, a - (n-3)^2 неположительно для любого n, то наибольшей сумма будет тогда, когда наибольшим будет первое слагаемое, т.е. когда - (n-3)^2 = 0, при n = 3.
В этом случае Sn = - (n-3)^2 + 9 = 0 + 9 = 9.
Объяснение:
6. данная функция является сложной. корень четной степени - это значит, что значение под корнем должно быть неотрицательным. т.е.
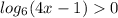решаем данное неравенство.
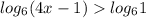
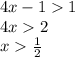
далее, функция логарифмическая, следовательно величина под знаком логарифма должна быть больше нуля.
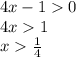
рассматриваем оба неравенства и находим область пересечения интервалов
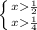x∈ [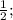 
+∞ [
7. 
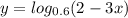значение под знаком логарифма должно быть больше нуля. 2-3х>0 2>3x x<2/3
рассмотрим условие при котором у>1
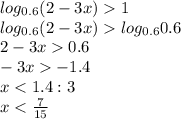
находим область пересечения обоих условий,
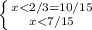x∈ ] -∞; 7/15 [
8. 
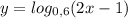область определения функции.
2х-1>0 x>1/2
вводим дополнительное условие
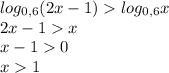
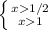x∈ ] 1; +∞ [
Объяснение:
а) 3x(x²y+2x+y³)
б)(3+2x)(x²-x(2x+3))= x(2x+3)(x-(2x+3)= x(2x+3)(x-2x-3)= -x(2x+3)(x+3)