Д) 4х > 12(3х – 1) – 16(х + 1);
е) а + 2 < 5(2а + 8) + 13(4 – а);
ж) 6у – (у + 8) – 3(2 – у) ≤ 2;
з) а(а – 4) – а2 > 12 – 6а;
и) (2х – 1) 2х – 5х < 4х2 – х;
к) 5у2 – 5у(у + 4) ≥ 100;
л) 6а(а – 1) – 2а(3а – 2) < 6;
решите неравенства осталось только 10 минут
.
 км/мин.
км/мин.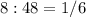 км/мин.
км/мин.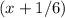 км/мин.
км/мин.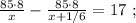
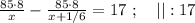
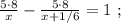
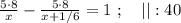
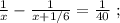
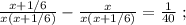
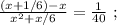
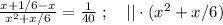
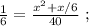
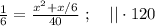
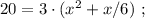
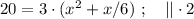
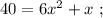
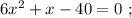
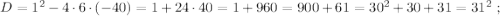
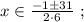
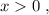 так, как это скорость,
так, как это скорость,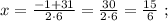
Выразим а2, а4 , а6 через первый член арифметической прогрессии и разность прогрессии (d)
a2=a1+d a4=a1+3d a6=a1+5d и подставим в систему:
{a1+a1+5d=11 a1+d+a1+3d=10
{2a1+5d=11 2a1+4d=10
Решим систему методом сложения. Умножим первое уравнение на (-1) и сложим со вторым:
{-2a1-5d=-11 + 2a1+4d=10
-d=-1
d=1
2a1+4=10
a1=3 (подставили найденное значение d во второе уравнение системы и нашли первый член прогрессии.)
По формуле суммы n-первых членов прогрессии найдём сумму первых шести членов этой прогрессии:
S6=(2·3+5 )\2·6=33 (Sn=(2a1+d(n-1))\2·n)
ответ:33