Уравнение параболы у= ах² + вх + с.
Один параметр вытекает из задания: параметр "с" равен ординате точки пересечения оси Оу: с = 1.
Далее используем формулу определения абсциссы вершины параболы: хо = -в/2а,
-2 = -в/2а, отсюда в = 4а.
Теперь используем данные точки (2; 7).
7 = а*2² + (4а)*2 + 1,
12а = 6,
а = 6/12 = 1/2, в = 4а = 4*(1/2).
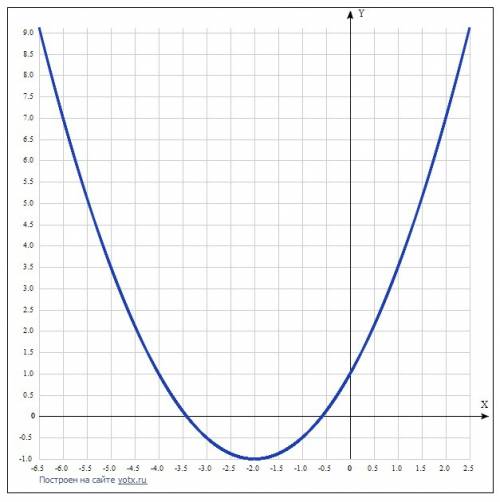
Получаем уравнение параболы у = (1/2)х² + 2х + 1.
Подставим абсциссу вершины хо = -2 и найдём её ординату:
уо = (1/2)*(-2)² + 2*(-2) + 1 = 2 - 4 + 1 = -1.
ответ: уо = -1.
Обозначим через x км/ч скорость теплохода в неподвижной воде. Тогда, его скорость по течению равна x+5 км/ч, а против течения x-5 км/ч. Сначала теплоход идет по течению реки 80 км, на которые он затратил часов. Затем, он стоит 23 часа, после чего движется в обратном направлении часов. В сумме он затратил на весь путь 35 часов. Получаем уравнение:
откуда
Решаем квадратное уравнение, получаем два корня:
Так как скорость теплохода не может быть отрицательным числом, то получаем ответ 15 км/ч.
ответ: 15.