Для начала найдём, при каких значениях m корни вообще есть. Для этого D≥0. Решая методом интервалов, получаем: . Это наша ОДЗ.
По теореме Виета Попробуем подогнать сумму квадратов корней под теорему Виета: Подставляем: Это парабола, ветви направлены вверх, значит, её точка минимума находится в её вершине. Если она принадлежит ОДЗ, то это и будет ответом, если нет - то либо 0, либо 0.75 (концы отрезков ОДЗ). - не подходит. Проверяем концы отрезков: При m = 0 сумма квадратов корней будет равна 2. При m = 0.75 сумма квадратов корней будет равна . Подходит первый вариант.
x^2+(m-3)x+m^2-6m-9.75=0 x^2+(m-3)x+m^2-6m+9-18.75=0 x^2+(m-3)x+(m-3)^2-18.75=0 D=(m-3)^2-4*((m-3)^2-18.75)=75-3*(m-3)^2=3*(5^2-(m-3)^2) решения действительны значит D>=0 значит -5 <= m-3 <= 5 значит -2 <= m <= 8 причем при m=-2 и m=8 имеем по одному корню вместо двух теперь т.Виетта x1+х2=-(m-3) x1*x2=(m-3)^2-18.75 x1^2+х2^2=(x1+х2)^2-2*x1*x2 = (m-3)^2-2(m-3)^2+2*18.75 = 37,5-(m-3)^2 поиск минимума функции f(m) = 37,5-(m-3)^2 на участке [-2;8] дает результат что 37,5-(m-3)^2 принимает максимальное значение при m=3 и равно 37.5 и что 37,5-(m-3)^2 принимает минимальное значение при m=-2 и m=8 и оно равно 13 заметим также что при m=-2 корень единственный х=-(m-3)/2=2,5; и сумма квадратов корней x^2=6,25 и при m=8 тоже корень единственный х=-(m-3)/2=-2,5; и сумма квадратов корней x^2=6,25 из вариантов m=-2 и m=8 выбираем максимальный m=8 - это ответ
![m\in(-\infty; 0]\cup[0.75; +\infty)](/tpl/images/0849/1100/e8c94.png)
. Это наша ОДЗ.
- не подходит. Проверяем концы отрезков:
. Подходит первый вариант.
Объяснение:
(х+3)²=16
по виете:
x1+x2=-6
x1*x2=9
x1=-3
x2=-3
по дискриминанту:
a=1 b=6 c=9
D=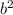
-4ac
D=36-4*1*9
D=0=0 ==> один корень
x=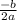
x=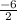
x=-3
ответ -3
(1-2x)(1+2x)=x
1-4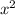
=x
-4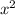
-x+1=0 ║*(-1)
4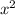
+x-1=0
a=4 b=1 c=-1
D=1+4*4*1
D=17
x1,2=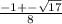
x1=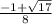
x2=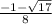
Отв: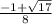
; 