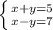
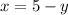
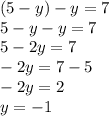
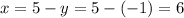
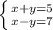
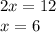
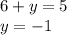
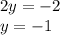
Відповідь:
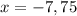
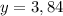
Пояснення:
Перетворимо рівняння системи. Обидві частини першого рівняння системи помножимо на 10, а друге - на 12, отримаємо наступну систему рівняння: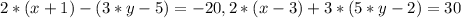 
Розкриємо дужки:
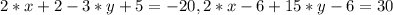
Зведемо подібні доданки в лівих частинах обох рівнянь системи, отримаємо:
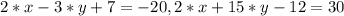
Значення зі змінної залишаємо в лівій частині, а вільні числа переносимо до правої частини, змінюючи знак на протилежний:
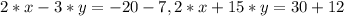
Виконуємо алгебраїчні обчислення в правих частинах обох рівнянь системи:
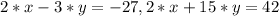
Помножимо обидві частини першого рівняння на 5, отримаємо рівняння:
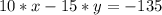
Використовуючи метод додавання, додамо обидві рівняння системи між собою, отримаємо:
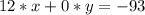
Знаходимо змінну 
:
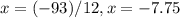
Підставимо змінну у будь-яке рівняння системи та знайдемо змінну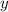 
, отримаємо:
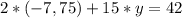
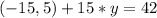
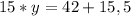
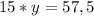
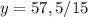
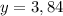
xy(x+y)-(x²+y²)(2x-y)=х²у+ху-(х²-у²)(2х-у)=х²у+ху²-(2х³-х²у-2ху²-у³)=х²у+ху²-2х³+х²у+2ху²-у=2х²у+3ху²-2х³-у³