сократите дроби (A^2N-B^2N)(A^2N-(AB)^N+b^2n)/A^3n+B

Question

Алгебра: сократите дроби (A^2N-B^2N)(A^2N-(AB)^N+b^2n)/A^3n+B

salome5toriy · Accepted Answer

Уравнение касательной к графику функции в точке имеет вид:

1. Вычисляем значение функции в точке :

н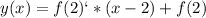 y(x)=f(2)`*(x-2)+f(2)

2. Вычисляем производную функции :

f(2)=1/3

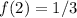
3. Вычисляем значение производной в точке :

(f(2))`=20

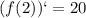
Таким образом, уравнение касательной имеет вид:

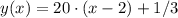
$y(x)=20 \cdot (x-2)+1/3$

Немного упрощая, получаем:

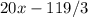
20x-119/3

ответ:

Уравнение касательной к графику функции в точке имеет вид:

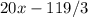
20x-119/3

Уравнение нормали к графику функции в точке имеет вид:

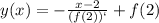
$y(x)=-\frac{x-2}{(f(2))`}+f(2)$

1. Вычисляем значение функции в точке :

f(2)=1/3

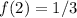
2. Вычисляем производную функции :

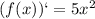
(f(x))`=5x^2

3. Вычисляем значение производной в точке :

(f(2))`=20

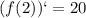
Таким образом, уравнение нормали имеет вид:

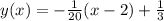
$y(x)=-\frac{1}{20}(x-2)+\frac{1}{3}$

Немного упрощая, получаем:

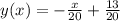
$y(x)=-\frac{x}{20}+\frac{13}{20}$

ответ:

Уравнение нормали к графику функции в точке имеет вид:

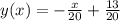
$y(x)=-\frac{x}{20}+\frac{13}{20}$