это "обманка"
задача "на внимание"
в обоих неравенствах слева стоят квадраты - они всегда больше равны 0
значит в первом неравенстве справа x - 3 >= 0 x>=3
во втором неравенстве 3 - x >= 0 x<=3
Значит решение может быть только x=3
надо проверить логарифмы - устраивает это или нет (так как других решений не может быть)
надо чтобы тело логарифма равнялась 1, тогда сам логарифм = 0
x^2 + 4x - 20 = 3^2 + 4*3 - 20 = 9 + 12 - 20 = 21 - 20 = 1
x^2 + 2x - 14 = 3^2 + 2*3 - 14 = 9 + 6 - 14 = 15 - 14 = 1
да оба логарифма = 0 и правые части = 0 при х=3
ответ х=3
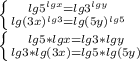
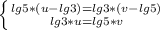
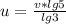
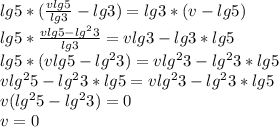
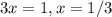 и
и 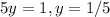
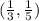
1)Координаты пересечения параболой оси Ох (-0,5; 0) (1; 0)
2)Координаты пересечения графиком оси Оу (0; 1)
Объяснение:
Найдите координаты точек пересечения параболы y= -2x²+х+1
с осями координат/
1)Чтобы найти точки пересечения параболы с осью Ох (нули функции), нужно решить квадратное уравнение:
-2x²+х+1 =0
2x²-х-1 =0
х₁,₂=(1±√1+8)/4
х₁,₂=(1±√9)/4
х₁,₂=(1±3)/4
х₁= -2/4= -0,5
х₂=4/4=1
Координаты пересечения параболой оси Ох (-0,5; 0) (1; 0)
2)Парабола пересекает ось Оу при х=0:
у= -2x²+х+1
у= 0+0+1
у=1
Координаты пересечения графиком оси Оу (0; 1)