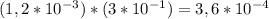Для того чтобы геометрическая прогрессия была бесконечно убывающей, знаменатель геометрической прогрессии 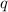 должен быть либо меньше 0, но больше -1, либо больше 0, но меньше 1. В таком случае геометрическая прогрессия будет стремиться к 0, но никогда его не достигнет.
должен быть либо меньше 0, но больше -1, либо больше 0, но меньше 1. В таком случае геометрическая прогрессия будет стремиться к 0, но никогда его не достигнет.
Графически это выглядит так: 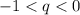 или
или 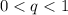 .
.
Рассмотрим наши примеры:
1) 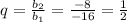 . Выполняются ли условия неравенства?
. Выполняются ли условия неравенства?
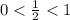 . Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
2) 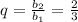 . Выполняются ли условия неравенства?
. Выполняются ли условия неравенства?
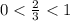 . Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
3) 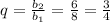 . Выполняются ли условия неравенства?
. Выполняются ли условия неравенства?
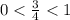 . Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
1)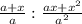
ответ: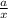
2)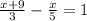
2x+45=15
2x=-30
x=-15
ответ: -15
3) 3x-4(x+1)<8+5x
3x-4x-4<8+5x
3x-4x-5x<8+4
-6x<12
x>-2
ответ: x>-2
4)