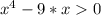
Раскладываем вторую скобку по формуле разности кубов
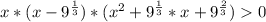
Заметим, что неполный квадрат в третьей скобке всегда положителен
Докажем это
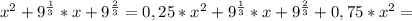
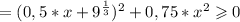
Так как квадраты не могут быть отрицательными.
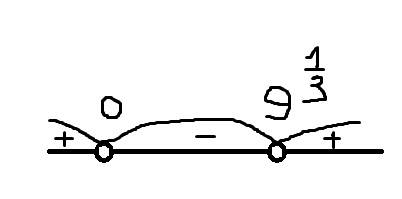
Значит можно рассмотреть неравенство методом интервалов.
1) При х<0 первый множитель будет меньше нуля, второй тоже меньше нуля. Два множителя меньше нуля дадут положительное число. А третий будет положительным. Значит все выражение в левой части будет положительным.
2) При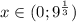 
Первый множитель будет больше нуля, второй меньше нуля, а третий как всегда положителен. Отрицательный множитель помноженный на положительные множители даст в итоге отрицательное число.
3) 
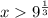
Первый множитель будет положителен, второй тоже положителен. А третий как всегда положителен. Значит в итоге, перемножив три положительных числа, получим положительное число.
В ответе получим два промежутка из первого и третьего случаев.
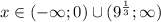
Заметно, что целочисленных решений будет бесконечно много. Это и все отрицательные целые числа и целые числа большие 2. Так как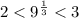 
Решений, так сказать, счетное множество.
Ну, а если бы был бы в неравенстве противоположный знак, то было бы всего два решения из второго случая. Это числа 1 и 2.
допустим монет по 2р.-х,а монет по 5р.-у
х+у=19
2х+5у=62
х=19-у х=19-у
2*(19-у)+5у=62 38-2у+5у=62
х=19-у х=19-у х=19-у
3у=62-38 3у=24 у=8
монет по 2р - восемь,а по 5р.- одиннадцать ( 19-8=11)