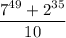 будет сократимой, если
будет сократимой, если 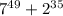 делится на
делится на 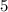 или
или 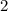 . А для того чтобы число делилось на
. А для того чтобы число делилось на 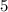 , нужно чтобы это число заканчивалось на
, нужно чтобы это число заканчивалось на 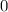 или на
или на 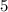 . А для делимости числа на
. А для делимости числа на 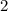 нужно чтобы число заканчивалось на четную цифру.
нужно чтобы число заканчивалось на четную цифру.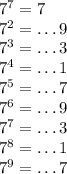
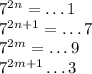
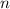 — чётное натуральное число,
— чётное натуральное число, 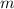 — нечётное натуральное число.
— нечётное натуральное число.
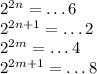
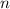 — чётное натуральное число,
— чётное натуральное число, 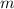 — нечётное натуральное число.
— нечётное натуральное число.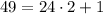 , то
, то 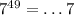 .
.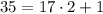 , то
, то 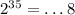 .
.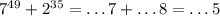 .
.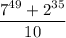 делятся на
делятся на 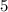 , значит, дробь сократима.
, значит, дробь сократима.
P.S. Если убрать последнюю -1, то останется конструкция, которая в математике называется интерполяционный многочлен Лагранжа, т.е. многочлен, график которого проходит через заданные точки плоскости. Тут это многочлен от а₀ степени х-1, проходящий через х точек (a₁,1),...,(аₓ,1). Такой многочлен тождественно равен 1, т.е. вся эта сложная сумма дробей - это запись константы 1 в виде многочлена степени x-1 от переменной a₀. Ну и в конце вычитаем 1 и получаем 0.