Квадратным трехчленом называют трехчлен вида a*x2 +b*x+c, где a,b,c некоторые произвольные вещественные (действительные) числа, а x – переменная. Причем число а не должно равняться нулю.Числа a,b,c называются коэффициентами. Число а – называется старшим коэффициентом, число b коэффициентом при х, а число с называют свободным членом.Корнем квадратного трехчлена a*x2 +b*x+c называют любое значение переменной х, такое, что квадратный трехчлен a*x2 +b*x+c обращается в нуль.Для того, чтобы найти корни квадратного трехчлена необходимо решить квадратное уравнение вида a*x2 +b*x+c=0.
Нахождение корней квадратного трехчлена по формуле.1. Найти значение дискриминанта по формуле D =b2-4*a*c.2. В зависимости от значения дискриминанта вычислить корни по формулам:Если D > 0, то квадратный трехчлен имеет два корня. x = -b±√D / 2*a Если D < 0, то квадратный трехчлен имеет один корень. x= -b / 2*aЕсли дискриминант отрицателен, то квадратный трехчлен не имеет корней Нахождение корней квадратного трехчлена выделением полного квадрата. Рассмотрим на примере приведенного квадратного трехчлена. Приведенное квадратное уравнение, уравнение у которого на старший коэффициент равен единице.Найдем корни квадратного трехчлена x2+2*x-3. Для этого решим следующее квадратное уравнение: x2+2*x-3=0; Преобразуем это уравнение:x2+2*x=3;В левой части уравнения стоит многочлен x2+2*x, для того чтобы представить его в виде квадрата суммы нам необходимо чтобы там был еще один коэффицент равный 1. Добавим и вычтем из этого выражения 1, получим:(x2+2*x+1) -1=3То, что в скобках можно представить в виде квадрата двучлена(x+1)2 -1=3;(x+1)2 = 4;Данное уравнение распадается на два случая либо x+1=2 , либо х+1=-2.В первом случае получаем ответ х=1, а во втором, х=-3.ответ: х=1, х=-3.В результате преобразований нам необходимо получить в левой части квадрат двучлена, а в правой части некоторое число. В правой части не должна содержаться переменная.
1) Пусть последовательность положительных чисел
является геометрической прогрессией, тогда
с формулы общего члена геометрической прогрессии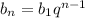
данную последовательность представим в виде:
2) Прологарифмируем по основанию
:
3) Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел.
. . . . . . . . . . . . . . . . . . . . . . . .
4) Рассмотрим полученную последовательность:
Очевидно, это арифметическая прогрессия, где
Доказано.