1. √(12×3)=6
2. 4√3 - 3√3 -√3 = 0
3. 9x²-4=0
x=±√(4/9)=±2/3
ответ: -2/3;2/3.
4. D=b²-4ac, где а - коэффициент перед х², b - коэффициент перед х, с - коэффициент без х
D=25-4×2×3=1
5.
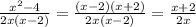
х≠2
При х=4(нужно просто подставить в формулу вместо х 4): 6/8=3/4
6. x1+x2=-b
x1x2=c, где b - коэффициент перед х, с - коэффициент без х
х1+х2=-7
7. х²-2х-3=0
х1+х2=2
х1х2=-3
ответ: -1;3.
8.
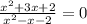
Корни первого уравнения: -2; -1, значит его можна записать как (х+2)(х+1)
Корни второго уравнения: -1; 2, значит его можна записать как (х+1)(х-2)

х≠-1; 2
х=-2
ответ: -2.
Если будут вопросы – обращайтесь :) Отметьте как лучший ответ, если не сложно ❤️
∫ x dx - 3∫ x^2 dx=1/2 x^2 - 3* 1/3 x^3= 1/2 x^2 - x^3 на пределах интегрирования получится 1/2 (2^2-1)- (2^3-1)=1/2*3-7 = -11/2
2. Здесь тоже довольно просто- нужно знать производную тангенса.
∫1/Cos^2(2x)dx= \делаем замену переменных: 2x=t, 2dx=dt\ = 1/2 ∫ 1/Cos^2[t] dt= 1/2 Tan[t], но уже на пределах от нуля до pi/3- посмотри на замену переменных. Тогда интграл будет равен 1/2(Tan[pi/3]-Tan[0])=√3/2
3. Здесь тоже не так трудно, как может показаться на первый взгляд
∫(2-3x)^5 dx = -1/(3*6) (2-3x)^6 на пределах интегрирования даст
-1/18 [ (2-3*1)^6-(2-3(1/3))^6 ] =-1/18 (1- 1)=0
4. Воспользовавшись четностью подынтегральной функции, можно записать как 2 интеграла от нуля до 3
2∫√(9-x^2)dx= \ x=3sint, dx=3cost dt\ = 2∫√(9-9sin^2(t)) cos(t) dt= 6∫√(1-sin^2(t)) cost dt= 18∫cos^2(t)dt=9∫(1+cos(2t))dt=9t+9/2sin(2t) на подстановке даст, учтя смену пределов интегрирования (t=pi/2, t=0) получим 9pi/2
5. По сути это уравнение в слегка усложненной записи.
Разделением интегралов на 2 и интегрированием, зная, что ∫x^p dx= 1/(p+1) * x^(p+1), получим 1/4(x^4)+5/2 x^2
На пределах интегрирования это даст
1/4( (a+2)^4- a^4) + 5/2 ((a+2)^2-a^2) = 4+8a+6a^2+2a^3 + 10+10a = 14+18a+6a^2+2a^3 = 0 по условию