Из исходного равенства видно, что p>q, в противном случае равенство не выполнялось бы. Предположим, что p=q+k, где k - натуральное. Тогда 2q+k=(q+k-q)^3, отсюда 2q+k=k^3 или 2q=k^3-k=k(k^2-1). Тогда q=k(k^2-1)/2. Отсюда сразу видно, что q будет простым только при k=2, поскольку при k=1 получаем 0, а при k>2 будем получать составные числа, а по условию q простое. Итак, при k=2, q=2*(2^2-1)/2=3. Тогда p=q+k=3+2=5. Это единственное решение удовлетворяющее данному равенству.
ответ: p=5, q=3.
p и q - простые => p + q > 0 => (p – q)³ > 0 => p – q > 0 => ∀ (p;q) ∃ n∈N: p – q = n => p = q + n
q+n+q=n^3 => q=(n^3-n)/2 => q = (n-1)n(n+1)/2
Из трех подряд идущих натуральных чисел одно делится на 3 => (n-1)n(n+1) ⁞ 3. Т.к. НОД(2, 3)=1, то q = (n-1)n(n+1)/2 ⁞ 3. Т.к. q простое, то q=3.
(n-1)n(n+1)=6
n натуральное => (n-1)³<6=>n-1<∛6<∛8=2 => n<2+1=3
n=1 => (n-1)n(n+1)=0≠6
n=2 => (n-1)n(n+1)=1*2*3=6 - верно => p=3+2=5 - простое
ответ: (5; 3)
№1
а) (x-4)^2=x^2-8x+16
б) (3x-5)^2=9x-30x=25
в) (2a-3)*(2a+3)=4a^2-9
г) (y^2-2)*(y^2+2)=y^4-4
№2
а) b^2-0.36=(b-0.6)*(b+0.6)
б) y^2-6y+9=(y-3)^2
№3
(2a-3b)*3b+(a-3b)^2
a=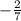
Упрощаем выражение:
6ab-9b^2+a^2-6ab+9b^2
Сокращаем все что сокращается:
a^2
Теперь решаем:
ответ: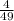
№4
а) 5(2-3xy)(2+3xy)=20-45x^2y^2
б) (a^3-b^2)^2=a^6-2*a^3*b^2+b^4
в) (x+y)^2-(x-y)^2=4xy
№5
(6a-1)(6a+1)-4a(9a+2)=-1
Упрощаем выражение:
-1-8a=-1
Данное уравнение не решаемо.
№6
(2x+3)(3x-7)-(x+1)(x-1)
Упрощаем выражение:
6x^2-5x-21-x^2+1
Снова упрощаем выражение:
5x^2-5x-20
Проверяем правильность утверждения что это выражение делится на 5 при любом целом "x"
Пусть x=8
Значит выражение теперь выглядит так:
(5*8)^2-5*8-20
Решать дальше смысла нет, так как при любом целом "x" последней цифрой будет ноль, значит выражение будет делится на 5.
Исключение это "x=1" в результате выражение будет равно 1.
Если это учесть то утверждение неверно!
Удачи, надеюсь