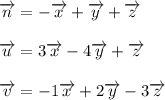
В базисе  векторы имеют следующие координаты:
векторы имеют следующие координаты:
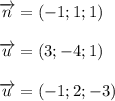
Их координаты попарно не пропорциональны, поэтому эти векторы не коллинеарны между собой.
Докажем компланарность векторов двумя
школьный (≈10 класс)
Признак компланарности трёх векторов:
Пусть векторы 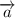 и
и 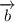 не коллинеарны. Если для вектора
не коллинеарны. Если для вектора 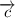 существует единственная пара реальных чисел A и B, такая, что
существует единственная пара реальных чисел A и B, такая, что 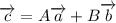 , то векторы
, то векторы 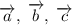 компланарны.
компланарны.
Покажем, что
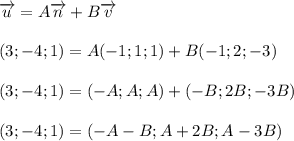
Слева и справа стоят координаты векторов. Векторы равны, если равны их соответственные координаты:
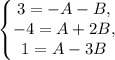
Сложим первое и второе уравнение, получим:
-1 = B
Подставим значение B в первое уравнение, найдём A:
3 = -A - (-1)
A = -2
Проверим найденные значения для остальных уравнений системы.
Итого получаем:
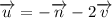
То есть признак выполнен. Значит векторы компланарны.
обычно проходится в вузах):
Векторы 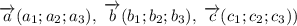 компланарны, если
компланарны, если
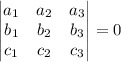
Проверим это условие для данных векторов:
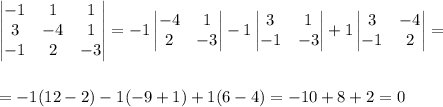
Следовательно, векторы компланарны.
Объяснение:
1. Найдите параболы, у которых ветви направлены вверх:
1) у =2х²; 2) у = (2-х)²; 3) у = 4 – 5х - х²; 4) у = х²+5х+4.
А) только 4); В) 1), 2); С) у всех; Д) 1), 2), 4).
Если перед х минус, то вниз, и наоборот.
2. Найдите координаты вершины параболы у = х²-4х+3.
А) (1;-4); В) (3;1); С) (-4;3); Д) (2;-1).
х= -в/2а=4/2=2 у=2^2-4*2+3=4-8+3= -1
3. Найдите ось симметрии параболы у = х²+2х+3.
А) х =0; В) х =1; С) х =2; Д) х = -1.
X= -в/2а= -2/2= -1
4. Найдите абсциссы точек пересечения графика функции у = х²+2,5х – 1,5 с осью Ох:
А) х = -1,5; х = -1; В) х =1,5; х = -1; С) х = -0,5; х = -3; Д) х = -3; х =0,5.
Нужно решить квадратное уравнение:
х²+2,5х – 1,5=0
х₁,₂=(-2,5±√6,25+6)/2
х₁,₂=(-2,5±√12,25)/2
х₁,₂=(-2,5±3,5)/2
х₁= -6/2= -3
х₂=1/2=0,5
5. Найдите координаты точек пересечения графика функции у = - х²+2х-3 с осью ординат:
А) (0;3); В) (0; -3); С) (-1; 3); Д) (1; -3).
График пересекает ось Оу при х=0:
у=0+0-3
у= -3
6. Как можно получить график функции у = х²-5 из графика функции у = х², сдвигая его вдоль оси:
А) Оу на 5 единиц вверх;
В) Оу на 5 единиц вниз;
С) Ох на 5 единиц вправо;
Д) Ох на 5 единиц влево.
7. График функции у = (х+3)² можно получить из графика функции у = х² сдвигом вдоль оси:
А) Ох на 3 единицы вправо;
В) Ох на 3 единицы влево;
С) Оу на 3 единицы вниз;
Д) Оу на 3 единицы вверх.
8. Сколько точек пересечений имеют графики функций у = х²+4х +4 и у = - х²-2х +1:
А) Не имеют точек; В) Одну точку;
С) Две точки; Д) Бесконечное множество.
9. Разложите на множители квадратный трехчлен 2 х² - 10х+12:
А) (2х – 4)(х+3); В) 2(х – 2)(х -3);
С) 2(х+2)(х+3); Д) (х -2)(х -3).
10. Сократите дробь Дроби не вижу, только ответы.
А) ; В) ; С) ; Д) .