![Решить уравнения: [tex]1) \sqrt{16 {x}^{2} + 16x + 29} = 5 \\ 2) \sqrt{9 {x}^{2} - 12x + 85} = 9[/te](/tpl/images/0125/1768/4eac2.jpg)
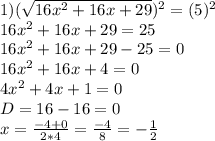
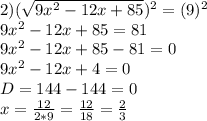
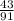
Объяснение:
Всего шаров 6+8 = 14
Вероятность того, что первый шар будет черным:
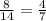
После того, как вынули черный шар, в ящике осталось 13 шаров, из которых 7 черных.Теперь вероятность того, что вытянутый шар будет черным:
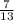
Вероятность того, что оба вынутых шара будут черными:
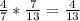
Теперь вычислим вероятность вынуть два белых шара.
Вероятность вынуть белый шар:
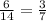
Вероятность вынуть второй белый шар:
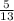
Вероятность того, что оба вынутых шара будут белыми:
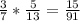
Теперь наконец-то вычислим вероятность того, что вынут два шара одного цвета (т.е. вынут два черных шара или два белых шара), используя правило сложения:
 .
.
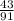
Объяснение:
Всего шаров 6+8 = 14
Вероятность того, что первый шар будет черным:
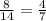
После того, как вынули черный шар, в ящике осталось 13 шаров, из которых 7 черных.Теперь вероятность того, что вытянутый шар будет черным:
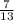
Вероятность того, что оба вынутых шара будут черными:
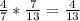
Теперь вычислим вероятность вынуть два белых шара.
Вероятность вынуть белый шар:
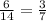
Вероятность вынуть второй белый шар:
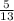
Вероятность того, что оба вынутых шара будут белыми:
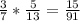
Теперь наконец-то вычислим вероятность того, что вынут два шара одного цвета (т.е. вынут два черных шара или два белых шара), используя правило сложения:
 .
.