Рисунок смотрите в приложении (на нем изображены равные векторы).
Векторы равны, когда они имеют равные длины и одинаковое направление (и при этом лежат на параллельных прямых или на одной и той же прямой).а). Векторы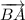 
и 
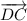равны по модулю (то есть, равны их длины), как стороны квадрата, но имеют разное направление. Как видно из рисунка, угол между ними равен 
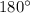градусов (получаем, что это коллинеарные, но не равные векторы).
.
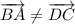б). Векторы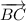 
и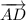 
равны по длине, лежат на параллельных прямых и имеют одинаковое направление. Значит, они равны.
.
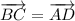в). Векторы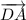 
и 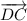опять же имеют одинаковые длины. Но они никак не лежат на параллельных прямых, они являются перпендикулярными (так как угол квадрата - 
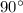градусов).
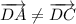
а) нет;
б) да;
в) нет.
Необходимо начертить вектор АВ=(2;4) . Начало вектора выбрать произвольно.
Координаты вектора - это проекции вектора на оси ОХ и ОУ. То есть вектор АВ проектируется на ось ОХ в отрезок , длина которого равна 2 единицам, а на ось ОУ - в отрезок, длина которого 4 единицы. Причём, так как координаты положительные, то направление от проекции начала вектора к проекции конца вектора такое же, как и у осей координат.
Если , например, за начало вектора возьмём точку А(2,1), то от точки А₁(2,0) , которая является проекцией точки А на ось ОХ, отложим вдоль оси ОХ отрезок длиной 2 единицы в направлении оси ОХ, попадём в точку В₁(4,0), которая будет проекцией точки В на ось ОХ. А₁В₁ - проекция вектора АВ на ось ОХ.
Аналогично, от точки А₂(0,1) отложим вдоль оси ОУ отрезок длиной 4 единицы, попадём в точку В₂(0,5) . А₂В₂ - проекция вектора АВ на ось ОУ.
Затем соединим точку А(2,1) с точкой В(4,5), получим искомый вектор АВ=(2,4).