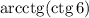
Известно соотношение:
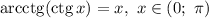
Кроме этого, известно, что основной период котангенса равен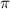 
:
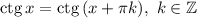
Таким образом, аргумент 6 нужно заменить некоторым аргументом вида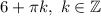 
, чтобы с одной стороны котангенсы этих аргументов были равны, а с другой стороны полученный аргумент удовлетворял формуле для простого нахождения арккотангенса от котангенса.
Запишем неравенство:
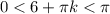
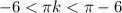
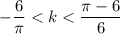
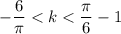
Выполним оценку обеих частей неравенства:
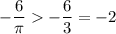
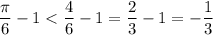
Получим:
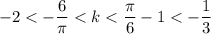
Или записывая соотношение для k:
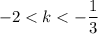
Единственное подходящее целое значение: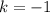 
.
Запишем:
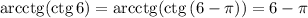
Действительно, 
, арккотангенс может принимать такое значение.
ответ: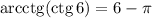 
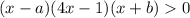
Нули выражения, записанного слева: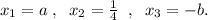 
Решение неравенства имеет вид: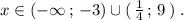 
Знаки выражения, записанного слева, чередуются таким образом;
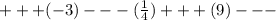
Поэтому в условии надо перед всей левой частью поставить знак минус, или записать неравенство со знаком меньше, а не больше.
То есть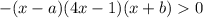 
или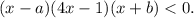 
.
Тогда возможен вариант ответа: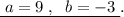 
.
Вид неравенства: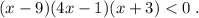 
P.S. Либо неравенство можно было записать , например, так:
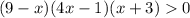или так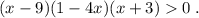 
Но заданное неравенство не будет иметь тот ответ, что записан в условии . Наверное, произошла описка и неравенство было задано со знаком меньше, а не больше.
двумя цифрами мы можем записать 99 чисел, а квартир 96, значит хватит