Question

Ділення многочленів 12х2-5х-7х3+3+3х4/3+х2-2х /-ділення !

Answer 1

Выполнить деление многочленов

$A=12x^{2}-5x-7x^{3}+3+3x^{4}:3+x^{2}-2x$

1) Расположим слагаемые в многочленах в порядке убывания степеней переменной х:

делимое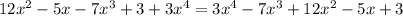 $12x^{2}-5x-7x^{3}+3+3x^{4}=3x^{4}-7x^{3}+12x^{2}-5x+3$

делитель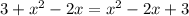 $3+x^{2}-2x=x^{2}-2x+3$

2) Разделим первый член делимого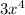 $3x^{4}$ на первый член делителя 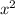$x^{2}$. В результате находим первый член частного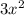 $3x^{2}$

3) Умножим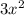 $3x^{2}$ на делитель и полученный результат 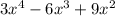$3x^{4}-6x^{3}+9x^{2}$ вычтем из делимого. Имеем

$-x^{3}+3x^{2}-5x+3$.

4) Разделим первый член результата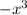 $-x^{3}$ на первый член делителя 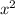$x^{2}$, находим 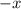$-x$ - второй член частного.

5) Умножим второй член частного на делитель и полученное произведение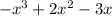 $-x^{3}+2x^{2}-3x$ - вычтем из результата третьего пункта. Имеем

$x^{2}-2x+3$.

6) Разделим результат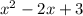 $x^{2}-2x+3$ на делитель 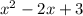$x^{2}-2x+3$. Получим 1 - третий член частного. Остаток от деления равен 0.

На письме деление выглядит так:

  3х⁴-7х³+12х²-5х+3Iх²-2х+3

- 3х⁴-6х³+9х²          I3х²-х+1

       -х³+3х²-5х+3     

    -  -х³+2х²-3х      

              х²-2х+3     

           -  х²-2х+3

                        0