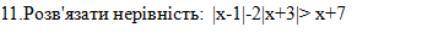
Дана система ур-ний 2x−y=19x−2 5y=14 Приведём систему ур-ний к каноническому виду −17x−y=−2 5y=14 Запишем систему линейных ур-ний в матричном виде [−17−1−20514] В 1 ом столбце [−170] делаем так, чтобы все элементы, кроме 1 го элемента равнялись нулю. - Для этого берём 1 ую строку [−17−1−2] , и будем вычитать ее из других строк: Во 2 ом столбце [−15] делаем так, чтобы все элементы, кроме 2 го элемента равнялись нулю. - Для этого берём 2 ую строку [0514] , и будем вычитать ее из других строк: Из 1 ой строки вычитаем: [−17−0−1−−1−2−−145]=[−17045] получаем [−170450514] Все почти готово - осталось только найти неизвестные, решая элементарные ур-ния: −17x1−45=0 5x2−14=0 Получаем ответ: x1=−485 x2=145
Объяснение:
ответы:
А1. 2) 13√3.
А2. 9;
А3. √8+√2;
А4. -10√ху;
А5. 3/(2+√х);
В1. 3(3х-5);
В2. 6 -20√5.
Объяснение:
А1. Упростите выражение:
√12 + 5√27 - √48=√4*3+5√9*3-√16*3=2√3+5*3√3-4√3=(2+15-4)√3=13√3.
***
А2. Найдите значение выражения
(√7 - √2 )(√7 - √2 ) + √56= √7√7-√7√2-√7√2+√2√2+=7-2√14+2-2√14=9-2√14+2√14=9;
***
А4. Упростите выражение:
(√5х -√5У) (√5х - √5У) – 5(х + У)= √5х√5х-√5х√5у-√5х√5у+√5у√5у-5х-5у= 5х-5√ху-5√ху+5у-5х-5у= -10√ху.
***
А5. Сократите дробь:
(6-3√Х)/(4- Х)=3(2-√х)/(2-√х)(2+√х)=3/(2+√х).
***
Дополнительная часть.
В1. Разложите на множители выражение:
9х – 15=3(3х-5).
***
В2. Выполните действия:
-√20 (√5 √( 20) ) + √12 ∙ √3= - (√20√5√20)+2√3√3= - 20√5+6 =6 -20√5
Привет, к сожалению у этого неравенства нет корней.
График данной функции выглядит так: (см. фото)
При значении функции Y больше 0, график не существует.