Чтобы уравнение имело корни нужно чтобы дискриминант был неотрицательным: .
Если дискриминант равен 0 ( при ), то уравнение имеет единственное решение . Поскольку 0,5 > 0, значение параметра пойдет в ответ.
Если дискриминант положителен (при ), то уравнение имеет 2 корня. Расписывать их необязательно.
Чтобы ровно один корень из двух был положителен необходимо и достаточно того, чтобы произведение корней было отрицательным.
Если - корни уравнения, то по теореме Виета
Нужно учесть, что должно также выполняться условие , так как в противном случае вещественных корней уравнение иметь не будет. Промежуток включает в себя промежуток , поэтому все значения параметра также пойдут в ответ.
ОТВЕТ можно записать в двух видах: при и ; при {}.
1)в) 2)б) 3)на нуль делить нельзя (? нет такого ответа) 4)а) 5)1-(х-3)/2=(2-х)/3 + 4 проведём к общему знаменателю (6) 6-3х+9=4-2х+24 -3х+2х=24-6-9 -х=9 х= -9 6)график - прямая линия задаём две точки х=0;-3,5 у=-3,5;0 строим их на координатной плоскости,проводим через них прямую. при х= -2,5 у = -1! 7)Пусть на шапку ушло х г,тогда на шарф 5х (г),а на рукавицы (х-5)(г),зная,что всего ушло 555 (г) составим и решим уравнение 5х+х+х-5=555 7х=555+5 7х=560 х=560÷7 х=80 (г)-на шапку 5×80=400 (г)-шарф 80-5=75 (г)-рукавицы
Формула квадратичной функции — формула вида y=ax²+bх+c Пересечение графика с осью абсцисс (т.е. с горизонтальной) — это корни уравнения ax²+bx+c=0 Корни уравнения в данном случае — это 5 и (-1) По теореме Виета в уравнении ax²+bx+c=0: с=5*(-1)=-5, -b=5-1=4, т.е. b=-4 Экстремум квадратичной функции — это вершина параболы. Вершина параболы находится по формуле ув.=(4ac-b²)/(4a), где ув. — координата вершины по игрику. Нам известны yв., в и с. Cоставим уравнение. -9=(4*a*(-5)-16)/(4a) … a=1 ответ: y=x²-4x-5.
Уравнение - квадратное вида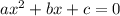 . Здесь
. Здесь 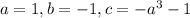 .
.
Чтобы уравнение имело корни нужно чтобы дискриминант был неотрицательным: .
.
Если дискриминант равен 0 ( при![a=-\frac{\sqrt[3]{10} }{2}](/tpl/images/1359/3684/650cc.png) ), то уравнение имеет единственное решение
), то уравнение имеет единственное решение 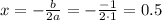 . Поскольку 0,5 > 0, значение параметра
. Поскольку 0,5 > 0, значение параметра ![a=-\frac{\sqrt[3]{10} }{2}](/tpl/images/1359/3684/650cc.png) пойдет в ответ.
пойдет в ответ.
Если дискриминант положителен (при![a-\frac{\sqrt[3]{10} }{2}](/tpl/images/1359/3684/a9de6.png) ), то уравнение имеет 2 корня. Расписывать их необязательно.
), то уравнение имеет 2 корня. Расписывать их необязательно.
Чтобы ровно один корень из двух был положителен необходимо и достаточно того, чтобы произведение корней было отрицательным.
Если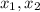 - корни уравнения, то по теореме Виета
- корни уравнения, то по теореме Виета 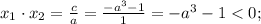
Нужно учесть, что должно также выполняться условие![a-\frac{\sqrt[3]{10} }{2}](/tpl/images/1359/3684/a9de6.png) , так как в противном случае вещественных корней уравнение иметь не будет. Промежуток
, так как в противном случае вещественных корней уравнение иметь не будет. Промежуток ![(-\frac{\sqrt[3]{10} }{2}; +\infty)](/tpl/images/1359/3684/921c4.png) включает в себя промежуток
включает в себя промежуток 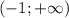 , поэтому все значения параметра
, поэтому все значения параметра 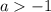 также пойдут в ответ.
также пойдут в ответ.
ОТВЕТ можно записать в двух видах: при![a=-\frac{\sqrt[3]{10}}{2}](/tpl/images/1359/3684/f1e21.png) и
и 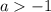 ; при
; при 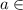 {
{![-\frac{\sqrt[3]{10}}{2}](/tpl/images/1359/3684/9e7d0.png) }
}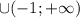 .
.