Область определения для первого уравнения: 13 - x > 0 x < 13
Область определения для второго уравнения: 2x - 1 ≥ 0 2x ≥ 1 x ≥ 0,5
Функция y = log₂(13 - x) убывает на всей своей области определения. Функция y = √(2x - 1) возрастает на всей своей области определения Значит, графики функций пересекутся в одной точке. Будем искать значения сначала в натуральных числах: x = 1: log₂12 ≠ 1 x = 2: log₂11 ≠ √3 x = 3: log₂10 ≠ √5 x = 4: log₂9 ≠ √7 x = 5 log₂8 = 3 Значит, x = 5 является решением системы. Остальные значения просматривать не нужно, т.к. мы уже показали, что будет единственное решение у системы. ответ: (5; 3).
Объяснение:
Здравствуйте!
Преобразуем функцию:
Найдем наименьшее значение функции:
То есть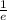 - точка минимума.
- точка минимума.
Поскольку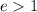 , то
, то 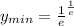
Если вам понравился ответ, сделай его лучшим.